инновационный подход к классификации данных, позволяющий решать сложные задачи машинного обучения с высокой точностью. В отличие от традиционного дерева решений, где одна ветвь представляет собой комбинацию нескольких классов, этот алгоритм создает отдельные ветви для каждого класса, учитывая их уникальные особенности и характеристики.
Такой подход позволяет улучшить качество предсказаний и сделать классификацию более точной и надежной. Каждая ветвь дерева решений относится к конкретному классу и основывается на его уникальных признаках. Это позволяет использовать разные алгоритмы и методы обработки для каждого класса, что увеличивает гибкость и адаптивность алгоритма к различным типам данных.
Такой подход имеет ряд преимуществ.
Во-первых, он позволяет точнее определить каждый класс и выявить его уникальные характеристики. Во-вторых, алгоритм может работать с большим количеством классов, что упрощает решение сложных задач классификации. Наконец, этот подход позволяет легко внедрять изменения и модифицировать классификацию в зависимости от изменяющихся условий и требований.
Алгоритм – строитель дерева решений
Алгоритм построения дерева решений является одним из основных методов машинного обучения и широко применяется в различных областях, где необходимо принимать решения на основе описанных данных. Он основан на принципе разделения данных на классы и построении древовидной структуры, которая позволяет классифицировать новые данные.
Дерево решений представляет собой графическую модель, где каждый узел представляет собой признак или свойство, а ветви — возможные значения этого признака. Таким образом, каждая ветвь дерева определяет правило или условие, которое позволяет принять решение о классификации данных.
Алгоритм строит дерево последовательно, начиная с корневого узла. На каждом шаге выбирается признак, который наилучшим образом разделяет данные на классы. После выбора признака происходит разделение данных на соответствующие ветви дерева, которые представляют отдельные классы. Данный процесс повторяется рекурсивно для каждой ветви, пока не будет достигнут критерий остановки.
Одним из основных критериев остановки является достижение максимальной глубины дерева или минимального числа объектов в каждом узле. Это позволяет избежать переобучения модели и сделать ее более обобщающей.
Построенное дерево решений представляет собой набор правил, с помощью которых можно классифицировать новые данные. Для этого необходимо пройти по правилам, начиная с корневого узла, и принять решение на основе условия, которое удовлетворяет значениям признаков нового объекта.
Благодаря своей простоте и понятности, алгоритм дерева решений широко используется в различных областях, включая медицину, финансы, анализ данных и другие. Он позволяет автоматизировать процесс принятия решений и обнаруживать скрытые закономерности в данных.
Машинное обучение. Лекция 6. Деревья решений
Классы, ветви и правила
В задаче построения дерева решений классы представляют собой категории или группы, в которые мы хотим классифицировать данные. Классификация данных позволяет нам установить свойства и характеристики, которые отличают один класс от другого. Ветви представляют собой отдельные пути или направления, на которые мы разделяем наши данные в процессе построения дерева решений.
Каждая ветвь дерева решений имеет свои уникальные правила, которые определяют, какие данные и каким образом будут отнесены к соответствующему классу. Эти правила могут быть основаны на различных признаках или атрибутах данных, таких как значение определенного признака или сравнение некоторых характеристик.
Правила разделения
Когда мы строим дерево решений, нам необходимо выбирать правило разделения ветвей. Это означает, что мы должны определить, какие данные будут отнесены к одной ветви, а какие — к другой. Для этого мы можем использовать различные критерии, такие как энтропия или Gini-индекс, которые позволяют нам оценить информативность разделения данных.
Применение правил разделения позволяет нам эффективно классифицировать данные и построить дерево решений, которое максимально точно отражает характеристики и свойства каждого класса. Кроме того, правила разделения являются ключевым компонентом алгоритма построения дерева решений и позволяют нам последовательно создавать ветви для каждого класса.
Пример использования классов, ветвей и правил
Для наглядности рассмотрим простой пример. Предположим, у нас есть набор данных о фруктах, и мы хотим классифицировать их как "яблоки" и "апельсины". Классы в данном случае — это сами "яблоки" и "апельсины". Мы можем построить дерево решений, где каждая ветвь представляет собой правило разделения данных.
Например, первое правило разделения может быть основано на цвете фрукта. Если фрукт красный, то он будет отнесен к классу "яблоки", а если он оранжевый, то к классу "апельсины". Затем мы можем применить другое правило разделения, например, на основе диаметра фрукта. Если диаметр фрукта меньше 5 см, то он будет отнесен к классу "яблоки", а если больше 5 см — к классу "апельсины".
Таким образом, использование классов, ветвей и правил позволяет нам эффективно разделять и классифицировать данные, создавая точное и информативное дерево решений.
Разделение данных на классы
Перед тем как приступить к построению дерева решений, необходимо разделить имеющиеся данные на классы. Для этого рассматриваемая задача должна иметь множество примеров, каждый из которых относится к определенному классу. Классы могут быть представлены как наборы объектов, имеющих схожие свойства или характеристики.
Разделение данных на классы является важным шагом в построении дерева решений, поскольку оно определяет, какие классы будут участвовать в создании отдельных ветвей дерева. Чем более разноплановыми и разнообразными окажутся классы, тем точнее и надежнее будет построенное дерево решений.
Чтобы разделить данные на классы, необходимо анализировать каждый пример и определить, к какому классу он принадлежит. Для этого можно использовать различные алгоритмы и методы классификации, включая статистические подходы, машинное обучение и др.
Примерами классов могут быть различные категории товаров в интернет-магазине (например, одежда, обувь, аксессуары), типы иконок на веб-сайте (например, домашняя страница, каталог продукции, контакты) или диагнозы заболеваний в медицине (например, грипп, ангина, пневмония).
Важно учитывать, что качество разделения данных на классы напрямую влияет на качество и эффективность построенного дерева решений. Чем более точно будет проведено разделение, тем более правильными будут принимаемые деревом решений решения.
Строим дерево для каждого класса
Строитель дерева решений — это алгоритм, который разделяет данные на отдельные классы путем создания ветвей в дереве. Каждая ветвь соответствует определенному классу данных, и внутри нее содержатся правила для классификации.
Для построения дерева решений для каждого класса, мы используем следующий алгоритм:
- Выбираем класс, для которого строим дерево.
- Отбираем только те данные, которые относятся к выбранному классу.
- Подготавливаем данные для построения дерева, удаляя ненужные атрибуты и приводя их к единому формату.
- Строим дерево решений используя выбранные данные.
- В каждой ветви дерева устанавливаем правила, которые позволят отнести новые данные к нужному классу.
Построение дерева решений для каждого класса позволяет нам более точно классифицировать данные. Каждое дерево будет специализироваться на определенном классе, что позволит нам получить более точные результаты.
Когда у нас есть отдельные деревья для каждого класса, мы можем использовать их вместе для классификации новых данных. Алгоритм определит, к какому классу относится новые данные, сравнивая их с правилами, установленными в каждой ветви дерева.
Построение отдельного дерева решений для каждого класса является одним из подходов к решению задачи классификации. Этот метод позволяет достичь высокой точности и обеспечивает гибкость в работе с различными классами данных.
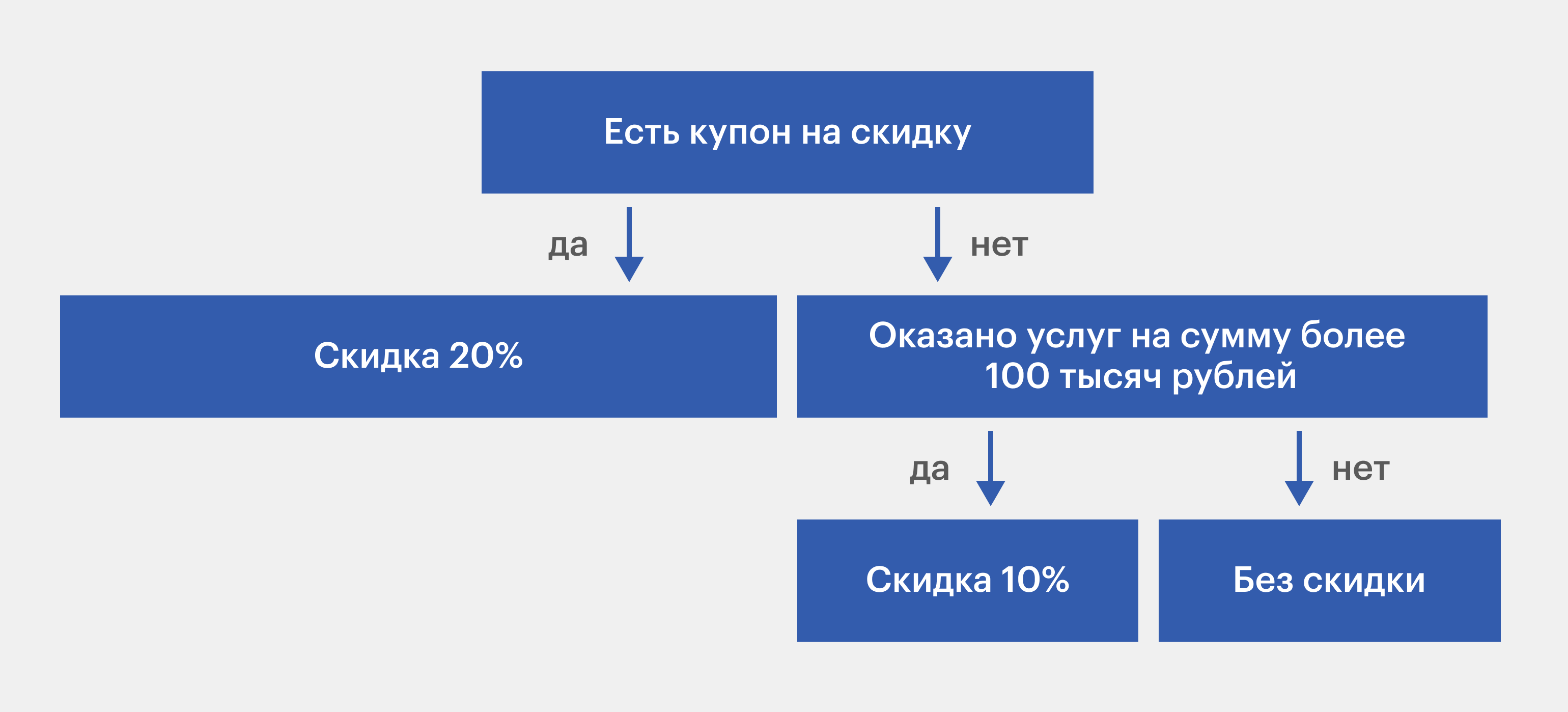
Выбираем правило для разделения ветвей
Один из ключевых шагов в построении дерева решений для каждого класса — это выбор правила для разделения ветвей. Правило определяет, как будет происходить разделение данных на классы, чтобы в результате получить наиболее точную классификацию.
При выборе правила для разделения ветвей, алгоритм учитывает различные факторы, такие как релевантность признаков и их влияние на классификацию. Алгоритм строит различные критерии, которые помогают определить, какое правило лучше всего подходит для разделения ветвей.
Меры неоднородности
Одним из основных критериев, используемых в алгоритме, являются меры неоднородности. Эти меры позволяют оценить степень различия между классами на основе различных признаков. Чем меньше значение меры неоднородности, тем более четко можно разделить данные на классы.
Существует несколько различных мер неоднородности, которые могут быть использованы в алгоритме выбора правила для разделения ветвей. Некоторые из них включают в себя энтропийный критерий, критерий Джини и критерий информативности.
Энтропийный критерий
Энтропийный критерий измеряет степень неопределенности в системе. Он определяет, насколько случайна классификация данных и позволяет оценить, насколько важен каждый признак для классификации. Чем меньше энтропия, тем лучше правило для разделения ветвей.
Критерий Джини
Критерий Джини оценивает вероятность ошибки при классификации, если случайно выбрать объект из выборки и присвоить его случайному классу. Он позволяет оценить, насколько хорошо каждый признак разделяет классы. Чем меньше значение критерия Джини, тем лучше правило для разделения ветвей.
Критерий информативности
Критерий информативности оценивает количество информации, которое приобретается при разделении выборки по определенному признаку. Он позволяет определить, насколько каждый признак помогает улучшить классификацию. Чем больше значение критерия информативности, тем лучше правило для разделения ветвей.
В процессе выбора правила для разделения ветвей, алгоритм анализирует значения всех вышеперечисленных критериев и выбирает правило, которое наиболее эффективно разделяет данные на классы. Это позволяет построить качественное дерево решений, которое хорошо классифицирует объекты.
Создаем отдельные ветви для каждого класса
Теперь, когда мы разделили данные на классы и построили дерево для каждого класса, настало время создать отдельные ветви для каждого класса. Это важный шаг в алгоритме построения дерева решений, который позволяет нам провести классификацию данных.
Каждая ветвь представляет собой правило, которое определяет, какие данные будут переходить к следующему узлу дерева. Ветви создаются на основе признаков и их значений, в которых мы разделили данные на предыдущем шаге. Например, если у нас есть признак "Возраст" и мы нашли разделение по значению 30, то создается две ветви: одна для данных с возрастом меньше или равным 30, и другая для данных с возрастом больше 30.
При создании ветвей мы не только разделяем данные на классы, но и учитываем их распределение в каждом классе. Это помогает нам строить более точные предсказания и определять более точные правила для разделения данных. Например, если у нас есть два класса: "Здоровые" и "Больные", и мы видим, что большинство данных с возрастом меньше 30 относятся к классу "Здоровые", то мы можем создать ветвь, которая будет отделять данные с возрастом меньше 30 и относящиеся к классу "Здоровые". Это поможет нам лучше классифицировать новые данные, основываясь на их признаках и значениях.
Таким образом, создание отдельных ветвей для каждого класса позволяет нам более эффективно провести классификацию данных и дает нам более точные правила для принятия решений. Использование алгоритма, который строит отдельные ветви дерева решений для каждого класса, является эффективным методом машинного обучения, который находит широкое применение в различных областях, включая медицину, банковское дело, рекламу и многое другое.