Дерево Хаффмана – это эффективная структура данных, которая используется для сжатия информации. Она была разработана американским математиком Дэвидом Хаффманом в 1952 году. Дерево Хаффмана позволяет представить исходные данные в более компактной форме, используя минимальное количество битов.
Основная идея дерева Хаффмана заключается в том, что часто встречающиеся символы в тексте должны занимать меньше места, чем редко встречаемые символы. Дерево Хаффмана строится на основе частотности символов в тексте: чем чаще символ встречается, тем ближе он будет к корню дерева.
Как работает дерево Хаффмана? В начале построения дерева каждый символ представляется в виде узла дерева. Затем узлы с наименьшей частотностью объединяются до тех пор, пока не будет сформировано само дерево, в котором каждый символ представлен своим уникальным кодом. Коды символов в дереве Хаффмана могут начинаться с 0 или 1, причем символы с большей частотностью будут иметь более короткие коды.
Дерево Хаффмана является одним из основных компонентов алгоритма сжатия данных. Оно применяется в различных областях, где требуется сокращение объема информации. Поэтому знание о дереве Хаффмана является важной составляющей компетенции в области информатики и программирования.
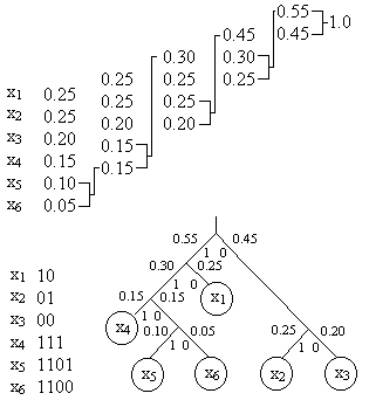
Определение дерева Хаффмана
Дерево Хаффмана – это бинарное дерево, которое используется для эффективного сжатия данных. Это особое дерево, где каждый узел представляет собой символ или комбинацию символов, а листья дерева соответствуют конкретным символам или символьным последовательностям.
Создание дерева Хаффмана
Для создания дерева Хаффмана необходимо проанализировать частоту встречаемости символов в исходном тексте или наборе данных. Символы с наибольшей частотой встречаемости получают меньшую длину кода, а символы с наименьшей частотой – большую длину кода. Это позволяет сократить общую длину кодов и обеспечить эффективное сжатие данных.
Создание дерева Хаффмана включает следующие шаги:
- Подсчет частоты встречаемости каждого символа в исходных данных.
- Создание отдельного дерева для каждого символа, присваивая им соответствующую частоту встречаемости.
- Объединение двух деревьев с наименьшей частотой встречаемости в одно дерево путем создания нового узла, суммирующего частоты.
- Повторение предыдущего шага до тех пор, пока все деревья не объединятся в одно дерево, содержащее все символы.
Кодирование символов
После создания дерева Хаффмана, каждый символ получает свой уникальный код, который представляет собой последовательность 0 и 1. Код каждого символа определяется его положением в дереве: если символ находится в левом поддереве, то к его коду добавляется 0, а если в правом – 1.
Благодаря конструкции дерева Хаффмана, кодирование и декодирование данных становятся эффективными и не требуют большого количества дополнительных битов для передачи информации. Этот алгоритм используется для сжатия данных во многих областях, таких как коммуникации, хранение информации и мультимедийные приложения.
Кодирование Хаффмана (пример)
Принцип работы дерева Хаффмана
Дерево Хаффмана — это особый вид бинарного дерева, используемый для эффективного сжатия данных. Оно основано на принципе оптимального кодирования символов с использованием переменной длины кодов. При сжатии данных дерево Хаффмана играет ключевую роль в создании кодового словаря, который определяет соответствие каждого символа определенному двоичному коду.
Принцип работы дерева Хаффмана заключается в следующем:
1. Подсчет частоты встречаемости символов
Первый шаг в создании дерева Хаффмана — подсчет частоты встречаемости символов в исходном наборе данных. Для этого проходится по всем символам и подсчитывается количество их вхождений.
2. Создание списка листьев дерева
Из полученной информации о частоте встречаемости символов создается список листьев дерева Хаффмана. Каждый лист представляет собой один символ и его частоту вхождений в исходные данные.
3. Объединение листьев в узлы дерева
Далее последовательно берутся два листа с наименьшей частотой встречаемости символов, создается новый узел-родитель для них. Частота нового узла равна сумме частот детей, а дети становятся левым и правым поддеревом родителя.
4. Повторение шагов 2-3 до создания корневого узла
Шаги 2 и 3 повторяются до тех пор, пока все листья не объединятся в один корневой узел дерева Хаффмана. Каждый новый узел также добавляется в список, чтобы сохранить структуру дерева.
5. Создание кодового словаря
Окончательный шаг — создание кодового словаря, который определяет двоичный код для каждого символа. Для этого происходит обход дерева Хаффмана, начиная с корневого узла. Путь от корня до каждого листа определяет двоичный код для символа.
Дерево Хаффмана обеспечивает эффективное сжатие данных, так как символы, которые часто встречаются, имеют более короткие коды, а редкие символы — более длинные коды. Это позволяет сократить количество бит, необходимых для представления исходных данных, и уменьшить объем передаваемой информации.
Реализация алгоритма дерева Хаффмана
Алгоритм дерева Хаффмана основан на построении оптимального префиксного кода для сжатия данных. Реализация этого алгоритма включает несколько ключевых шагов.
Шаг 1: Подсчет частоты символов
Первым шагом в реализации алгоритма дерева Хаффмана является подсчет частоты символов в тексте или файле, который нужно сжать. Это делается путем прохода по всем символам и увеличения счетчика для каждого символа.
Шаг 2: Создание листьев дерева
После подсчета частоты символов, создаются листья дерева Хаффмана. Каждый лист представляет собой символ и его частоту. Листы располагаются в порядке возрастания их частоты.
Шаг 3: Построение дерева Хаффмана
Следующий шаг — построение дерева Хаффмана с помощью следующего алгоритма:
1. Выбрать два листа с наименьшей частотой и создать новый узел, который будет служить их родителем.
2. Удалить выбранные листы из списка листьев и добавить новый узел.
3. Повторить шаги 1 и 2, пока в списке листьев не останется только один узел — корень дерева Хаффмана.
Шаг 4: Запись кодов Хаффмана
После построения дерева Хаффмана, необходимо записать коды Хаффмана для каждого символа. Код Хаффмана для каждого символа определяется путем перемещения от корня дерева к листьям и отметки каждого перехода 0 или 1 в зависимости от направления движения.
Таким образом, реализация алгоритма дерева Хаффмана включает подсчет частоты символов, создание листьев дерева, построение дерева Хаффмана и запись кодов Хаффмана. Этот алгоритм позволяет эффективно сжимать данные, сохраняя при этом информацию без потерь.
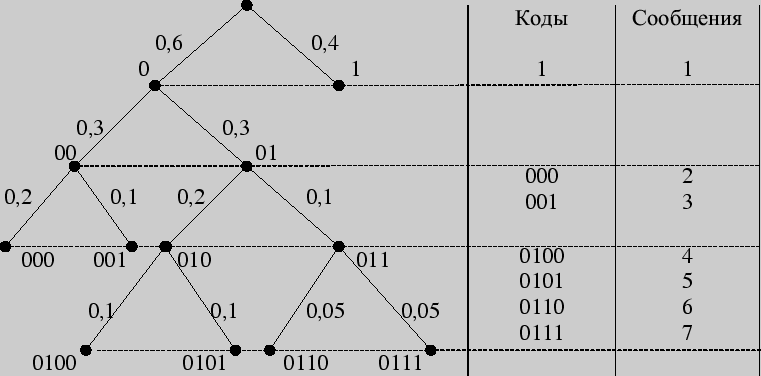
Применение дерева Хаффмана в сжатии данных
Дерево Хаффмана представляет собой эффективный алгоритм сжатия данных, который находит свое применение во многих областях, связанных с хранением и передачей информации. Одним из ключевых применений дерева Хаффмана является сжатие данных.
Принцип работы дерева Хаффмана
Дерево Хаффмана основано на принципе переменной длины кодирования символов в зависимости от их частоты встречаемости. Символы, которые часто встречаются, кодируются короткими последовательностями бит, а символы, встречающиеся редко, — длинными последовательностями бит.
Процесс сжатия данных с помощью дерева Хаффмана состоит из нескольких шагов:
- Подсчет частоты встречаемости каждого символа в исходном тексте.
- Построение дерева Хаффмана на основе частот символов.
- Присвоение двоичных кодов символам в соответствии с их положением в дереве Хаффмана.
- Замена каждого символа в исходном тексте его двоичным кодом.
- Сжатие данных путем объединения битовых последовательностей символов.
Применение дерева Хаффмана в сжатии данных
Дерево Хаффмана является основным алгоритмом сжатия данных, который используется во многих системах и форматах файлов. Он может быть использован для сжатия текстовых документов, аудио- и видеофайлов, изображений и многого другого.
Преимущества использования дерева Хаффмана в сжатии данных:
- Эффективность сжатия: дерево Хаффмана позволяет сжать данные без потери информации, достигая высокого уровня компрессии.
- Простота реализации: алгоритм дерева Хаффмана легко реализуем и может быть использован в различных программных приложениях.
- Быстродействие: сжатие данных с использованием дерева Хаффмана происходит быстро и эффективно.
Однако, дерево Хаффмана имеет и некоторые недостатки:
- Сложность реализации декодирования: необходимость построения дерева Хаффмана для декодирования данных может потребовать дополнительных ресурсов и времени.
- Зависимость от частоты символов: дерево Хаффмана может не эффективно сжимать данные, если частоты символов сильно отличаются или изменяются в процессе передачи данных.
В целом, дерево Хаффмана является мощным инструментом для сжатия данных, который позволяет сэкономить пропускную способность канала связи или объем хранения информации, не потеряв при этом ценную информацию.
Преимущества и недостатки дерева Хаффмана
Дерево Хаффмана является одним из наиболее эффективных алгоритмов сжатия данных. У него есть свои преимущества и недостатки, которые стоит учитывать при его использовании.
Преимущества дерева Хаффмана:
- Высокая степень сжатия данных: алгоритм Хаффмана способен сократить объем данных до минимально возможного размера. Он строит оптимальное дерево кодирования, в котором часто встречающиеся символы занимают меньшее количество бит, а редкие символы — больше. Это позволяет существенно сократить размер исходного файла.
- Быстрая скорость сжатия: дерево Хаффмана отличается относительно небольшим количеством операций, поэтому алгоритм работает достаточно быстро. Скорость сжатия данных с помощью дерева Хаффмана значительно превосходит другие алгоритмы сжатия, такие как алгоритм Лемпела-Зива и алгоритм RLE (Run-Length Encoding).
- Простота реализации: алгоритм Хаффмана имеет достаточно простую реализацию, что позволяет легко его реализовать на любом языке программирования. Он не требует большого количества памяти или сложных вычислений, поэтому его можно использовать на различных устройствах и платформах.
- Ориентация на работу с текстовыми данными: дерево Хаффмана хорошо подходит для сжатия текстовых данных, так как текст обычно содержит повторяющиеся символы и фразы. Алгоритм Хаффмана эффективно кодирует эти повторяющиеся элементы, что позволяет существенно уменьшить объем текстового файла.
Недостатки дерева Хаффмана:
- Потеря данных: при сжатии данных с помощью дерева Хаффмана может произойти небольшая потеря информации. Так как алгоритм работает на основе статистической информации о частоте встречаемости символов, некоторые редкие символы могут быть закодированы с помощью большего количества бит, что может повлечь искажение исходной информации.
- Неэффективность для некоторых типов данных: дерево Хаффмана может быть неэффективным для сжатия определенных типов данных, таких как изображения или звуковые файлы. Это связано с тем, что в таких файлах часто отсутствуют повторяющиеся элементы или они имеют сложную структуру, что затрудняет построение оптимального дерева кодирования.
Таким образом, дерево Хаффмана является эффективным алгоритмом сжатия данных с высокой степенью сжатия и быстрой скоростью работы. Однако, его потенциал может быть ограничен для определенных типов данных и есть некоторая вероятность потери информации в процессе сжатия.