Бинарное дерево — это структура данных, которая представляет собой иерархическую структуру, состоящую из узлов и ребер. Каждый узел в бинарном дереве может иметь не более двух потомков — левого и правого. Бинарное дерево широко используется в информатике и алгоритмах для решения различных задач, таких как поиск и сортировка данных, а также для представления иерархических отношений.
Построение бинарного дерева можно выполнить с использованием различных алгоритмов, один из которых — алгоритм вставки. Для построения бинарного дерева с помощью этого алгоритма необходимо выполнить следующие шаги:
- Создать корневой узел дерева.
- Вставить новый узел слева или справа от корневого узла, в зависимости от заданного критерия сравнения (например, сравнение по значению).
- Если узел уже существует, перейти к следующему узлу и повторить шаг 2.
- Повторять шаги 2-3 до вставки всех узлов.
В результате выполнения этих шагов мы получим готовое бинарное дерево, которое можно использовать для решения различных задач. Важно отметить, что алгоритм вставки позволяет строить дерево в оптимальном порядке, чтобы обеспечить быстрый доступ к данным и эффективные операции над ними.
Определение бинарного дерева
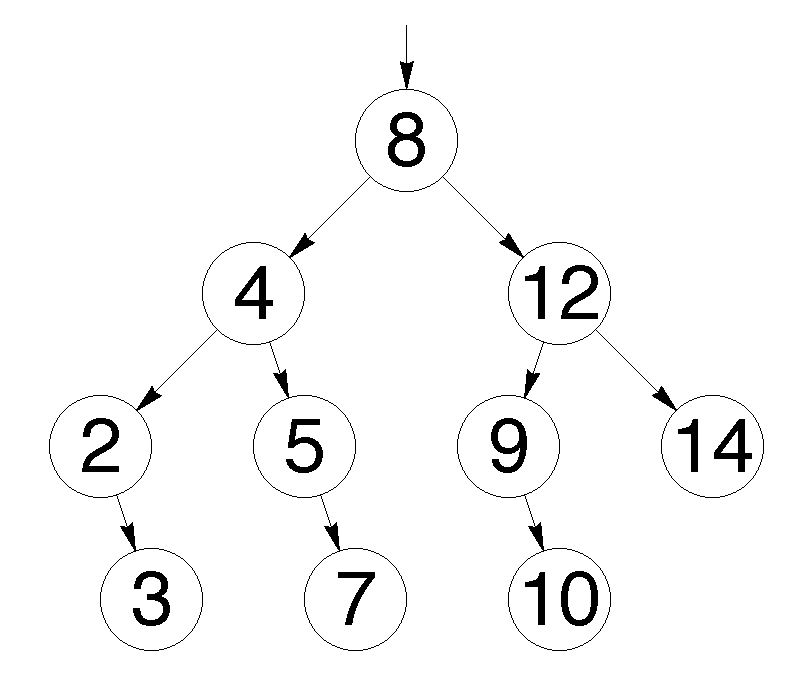
Бинарное дерево — это структура данных, которая состоит из узлов, связанных между собой с помощью ребер. Каждый узел в бинарном дереве может иметь максимум два потомка: левого и правого.
Узлы бинарного дерева можно представить в виде вершин, а ребра — в виде связей между этими вершинами. Каждый узел содержит значение и указатель на его левого и правого потомка. Вершина, не имеющая потомков, называется листом.
Бинарное дерево может быть пустым, то есть не содержать ни одного узла. В таком случае его корень указывает на null. Если бинарное дерево не пустое, то оно состоит из корня и поддеревьев, образованных левым и правым поддеревом корневого элемента.
Основные понятия бинарного дерева:
- Корень: вершина, являющаяся начальной точкой для поиска элементов в дереве;
- Левое поддерево: поддерево, образованное всеми элементами, находящимися слева от корня;
- Правое поддерево: поддерево, образованное всеми элементами, находящимися справа от корня;
- Дочерний узел: узел, который имеет непосредственную связь с другим узлом;
- Родительский узел: узел, который имеет непосредственную связь с дочерним узлом.
Бинарные деревья находят широкое применение в программировании и алгоритмах благодаря своей эффективности при поиске, вставке и удалении элементов. Они являются основой для реализации других структур данных, таких как бинарные кучи и бинарные поисковые деревья.
Структуры данных: Хранение полного бинарного дерева в массиве. Центр онлайн-обучения «Фоксфорд»
Выбор корневого элемента
При построении бинарного дерева необходимо выбрать корневой элемент, от которого будет производиться дальнейшее построение дерева. Выбор корневого элемента является одним из важных шагов при создании бинарного дерева и может оказывать значительное влияние на его эффективность и функциональность.
Корневой элемент бинарного дерева служит начальной точкой для построения дерева и определяет его структуру. Корневой элемент должен быть выбран таким образом, чтобы обеспечить равномерное распределение элементов и упорядоченность данных.
При выборе корневого элемента необходимо учитывать следующие факторы:
- Равномерность распределения элементов. Корневой элемент должен быть выбран таким образом, чтобы элементы были равномерно распределены по всему дереву. Это позволит достичь оптимальной производительности при выполнении операций поиска и вставки.
- Упорядоченность данных. Корневой элемент должен быть выбран таким образом, чтобы элементы в дереве были упорядочены. Это обеспечит возможность выполнения эффективного поиска элементов в дереве и упростит проведение операций сортировки и удаления элементов.
- Удобство работы с корневым элементом. Корневой элемент должен быть выбран таким образом, чтобы обеспечить удобство работы с данными. Например, если элементы в дереве имеют уникальные идентификаторы, можно выбрать корневой элемент с наименьшим идентификатором для облегчения поиска и вставки элементов.
Выбор корневого элемента является важным этапом при построении бинарного дерева. Правильный выбор корневого элемента с учетом равномерности распределения элементов, упорядоченности данных и удобства работы с данными позволяет создать эффективное и функциональное бинарное дерево.
Вставка элементов
Вставка элементов — одна из основных операций, выполняемых над бинарным деревом. При вставке нового элемента необходимо учитывать правила построения бинарного дерева.
При начале вставки происходит проверка наличия корневого элемента. Если дерево пустое, то новый элемент становится корневым.
Если дерево не пустое, то вставка происходит путем перебора элементов с учетом их значений. Новый элемент сравнивается с каждым элементом дерева, и в зависимости от результата сравнения выбирается направление перехода к следующему элементу.
Если новый элемент меньше текущего, то переход осуществляется к левому потомку. Если же новый элемент больше или равен текущему, то переход осуществляется к правому потомку.
Этот процесс повторяется до тех пор, пока не будет найдено место для вставки нового элемента. При этом учитывается, что в бинарном дереве не должно быть повторяющихся элементов.
После нахождения подходящей позиции новый элемент вставляется в соответствующее место и становится листом дерева.
Важно отметить, что при вставке элементов необходимо обеспечить соблюдение баланса дерева. Неправильная последовательность вставки элементов может привести к образованию дерева с большой высотой и, как следствие, к снижению эффективности работы с ним.
Вставка элементов в бинарное дерево является важной операцией, позволяющей эффективно добавлять новые элементы и сохранять упорядоченность структуры. Правильно реализованная вставка позволяет быстро находить и удалять элементы, а также обеспечивает эффективную работу с отсортированными данными.
Преимущества бинарных деревьев
Бинарные деревья являются одной из самых распространенных и полезных структур данных в информатике. Они обладают рядом преимуществ, которые делают их привлекательными для использования в различных задачах.
1. Эффективный поиск
Одним из основных преимуществ бинарных деревьев является быстрый поиск элементов. Благодаря упорядоченности структуры дерева, поиск элемента может выполняться за время, логарифмически зависящее от количества элементов в дереве. Это делает бинарные деревья идеальным выбором для задач, требующих быстрого поиска элементов.
2. Удобное управление данными
Бинарные деревья позволяют легко добавлять, удалять и модифицировать элементы. Вставка нового элемента или удаление существующего элемента происходит за время, логарифмически зависящее от размера дерева. Такой эффективный доступ к данным позволяет удобно управлять информацией в дереве и выполнять различные операции с ними.
3. Упорядоченность элементов
Бинарные деревья позволяют упорядочить элементы по различным критериям, в зависимости от потребностей задачи. Например, элементы можно упорядочить по возрастанию или убыванию. Упорядоченность элементов упрощает выполнение таких операций, как поиск минимального и максимального элементов, а также поиск элементов, соответствующих определенным условиям.
4. Гибкость и многообразие применений
Бинарные деревья могут использоваться в различных областях и задачах. Они являются основой для построения других структур данных, таких как красно-черные деревья или AVL-деревья. Бинарные деревья также могут быть использованы для реализации алгоритмов сортировки, поиска и обработки данных. Гибкость и многообразие применений делают бинарные деревья важным инструментом в программировании.
Выводя все преимущества вместе, можно сказать, что бинарные деревья представляют собой эффективную и удобную структуру данных, позволяющую быстро и эффективно управлять информацией. Их упорядоченность и гибкость позволяют решать различные задачи, делая бинарные деревья неотъемлемой частью программирования.
Быстрый поиск элементов
Бинарные деревья предоставляют эффективный способ поиска элементов. Они обладают особенностью, позволяющей быстро найти нужный элемент в отсортированной коллекции. Быстрый поиск осуществляется за счет балансировки дерева и учета структуры его узлов.
Данная особенность бинарных деревьев позволяет эффективно находить элементы в коллекции намного быстрее, чем в случае линейного поиска. В бинарном дереве каждый узел может иметь двух потомков — левого и правого. Порядок следования элементов определяется ключами, которые задаются при вставке элементов в дерево.
Для поиска нужного элемента в бинарном дереве, мы сравниваем его значение с значением текущего узла. Если оно меньше или больше, чем значение текущего узла, мы направляемся к левому или правому потомку соответственно. Таким образом, поиск осуществляется по принципу "разделяй и властвуй". За счет балансировки дерева и учета структуры узлов, время поиска элемента в бинарном дереве является логарифмическим, то есть пропорционально логарифму количества элементов в дереве.
Поэтому использование бинарных деревьев для поиска элементов позволяет достичь высокой эффективности операции поиска. Быстрый поиск элементов в бинарных деревьях особенно полезен в случаях, когда требуется многократно выполнять операцию поиска в отсортированной коллекции.

Эффективное удаление элементов
Эффективное удаление элементов является одним из ключевых преимуществ бинарных деревьев. Благодаря особенностям структуры дерева, операция удаления выполняется очень быстро и эффективно.
При удалении элемента из бинарного дерева необходимо учесть несколько случаев:
- Если удаляемый элемент является листом (не имеет потомков), то он просто удаляется из дерева. Нет необходимости в дополнительных операциях.
- Если удаляемый элемент имеет только одного потомка, то этот потомок заменяет удаляемый элемент, сохраняя структуру дерева.
- Если удаляемый элемент имеет двух потомков, то необходимо найти наименьший элемент в правом поддереве или наибольший элемент в левом поддереве и заменить им удаляемый элемент. Далее, этот наименьший или наибольший элемент удаляется из своего поддерева.
Эффективность операции удаления обеспечивается тем, что в бинарном дереве элементы хранятся в отсортированном порядке. При удалении элемента необходимо проходить по дереву всего лишь один раз, чтобы найти его место и выполнить соответствующие замены.
Эффективное удаление элементов делает бинарные деревья очень полезными во многих приложениях, таких как поиск, сортировка и управление данными. Они также находят широкое применение в базах данных, в том числе в реализации структуры B-дерева.
Примеры применения бинарных деревьев
Бинарные деревья имеют широкий спектр применений в различных областях информатики и программирования.
Вот несколько примеров:
- Хранение данных: Бинарные деревья используются для хранения больших объемов данных, таких как множества, словари и базы данных. Благодаря их структуре, бинарные деревья позволяют быстро находить, вставлять и удалять элементы.
- Сортировка: Бинарные деревья предоставляют эффективный способ сортировки данных. Они могут быть использованы для реализации алгоритмов сортировки, таких как сортировка слиянием и быстрая сортировка.
- Потоковая обработка данных: Бинарные деревья могут быть использованы для обработки данных в режиме реального времени. Они позволяют эффективно добавлять и удалять элементы, что делает их подходящими для решения задач потоковой обработки данных.
- Оптимальные коды: Бинарные деревья используются для создания оптимальных кодов в теории информации. Оптимальные коды помогают уменьшить объем передаваемых данных и улучшить эффективность передачи информации по сети.
- Анализ данных: Бинарные деревья используются для анализа данных в различных областях, включая машинное обучение, биоинформатику и финансовую аналитику. Они позволяют быстро выполнять поиск, сортировку и фильтрацию данных.
Это лишь некоторые примеры применения бинарных деревьев. Благодаря их универсальности и эффективности, они широко используются в различных областях информатики и программирования.
Шувалов Кирилл Сергеевич. Мастер-класс на тему: "Бинарное дерево поиска"
Поиск в отсортированных массивах
Отсортированные массивы являются одной из наиболее эффективных структур данных для поиска элементов. Этот метод поиска основан на использовании алгоритма бинарного поиска, который позволяет быстро найти нужный элемент в упорядоченном массиве.
Принцип работы алгоритма очень прост: нужно сравнивать искомый элемент с элементом в середине массива. Если они равны, то элемент найден и поиск завершается. Если искомый элемент меньше, то поиск продолжается в левой половине массива, иначе — в правой половине. Этот процесс повторяется, пока не будет найден искомый элемент или не будет достигнут конец массива.
Бинарный поиск имеет логарифмическую сложность времени, что гарантирует быстрый поиск даже в больших массивах. Например, для массива из 1000 элементов при помощи бинарного поиска можно найти элемент за не более 10 сравнений, что очень эффективно.
Однако следует отметить, что для использования бинарного поиска массив должен быть предварительно отсортирован. Если массив не отсортирован, перед применением алгоритма нужно выполнить сортировку, что может занять время.
Кроме того, бинарный поиск лучше всего подходит для статических массивов, т.е. таких, размер которых не меняется. При изменении размера массива потребуется перестраивать индексы и учетные данные, что может замедлить алгоритм.
Тем не менее, бинарный поиск является одной из наиболее эффективных стратегий поиска в отсортированных массивах и широко применяется в различных областях программирования и алгоритмических задачах.