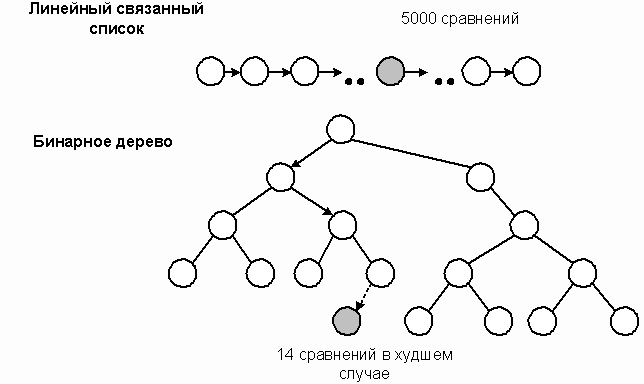
Бинарное дерево – это структура данных, состоящая из узлов, где каждый узел может иметь не более двух потомков. Такое дерево используется во множестве алгоритмов и программах для эффективной организации информации. Каждый узел бинарного дерева имеет определенные характеристики, которые помогают описать его и выполнить операции с данными.
Одна из важных характеристик бинарного дерева – глубина. Глубина дерева определяется как максимальное количество уровней, начиная от корневого узла и до самого дальнего листового узла. Чем больше уровней имеет дерево, тем больше данных оно может содержать и обрабатывать.
Другая важная характеристика – баланс. Бинарное дерево называется сбалансированным, если разница в глубине поддеревьев каждого узла не превышает некоторой заданной величины. Сбалансированное дерево обеспечивает эффективные операции поиска, вставки и удаления элементов.
Структура бинарного дерева
Бинарное дерево представляет собой абстрактную структуру данных, состоящую из узлов и ребер. Каждый узел в дереве может иметь не более двух потомков — левого и правого. Левый потомок, если он есть, находится слева от родительского узла, а правый потомок, если он есть, находится справа.
Структура бинарного дерева может быть представлена в виде комбинации узлов и связей между ними. Узел — это элемент дерева, который содержит некоторое значение и указатели на левого и правого потомка. Ребро — это связь между узлами, которая показывает направление от родительского узла к его потомку.
Корень бинарного дерева — это узел, который не имеет родителя и является самым верхним узлом в дереве. Листья — это узлы, которые не имеют потомков, то есть они находятся на самом нижнем уровне дерева.
Глубина бинарного дерева определяется как максимальная длина пути от корня до самого удаленного листа. Высота бинарного дерева — это максимальная глубина дерева, то есть количество уровней в дереве.
Особенностью бинарного дерева является то, что каждый узел имеет не более двух потомков. Это позволяет эффективно организовывать и хранить данные, а также выполнять различные алгоритмы поиска, добавления и удаления элементов.
Для работы с бинарными деревьями существуют различные алгоритмы, такие как обход дерева в глубину (префиксный, инфиксный, постфиксный обход) и обход дерева в ширину.
Бинарные деревья имеют широкое применение в информатике, например, для реализации структур данных, таких как бинарный поиск, куча, хеш-таблица и др.
Полное бинарное дерево и его свойства
Узлы и ребра
Бинарное дерево состоит из узлов и ребер. Узлы – это основные элементы структуры, которые содержат данные и связи с другими узлами. Ребра – это связи между узлами. Каждое ребро соединяет два узла: родительский и дочерний. Узел, с которого исходит ребро, называется родительским узлом, а узел, в который входит ребро, называется дочерним узлом. Бинарное дерево может иметь любое количество узлов и ребер, но каждый узел может иметь не более двух дочерних узлов.
Узлы бинарного дерева могут содержать различные типы данных: числа, строки, объекты и т.д. Каждый узел может быть уникальным и иметь свой уникальный идентификатор, что позволяет легко находить и работать с конкретным узлом.
Ребра бинарного дерева определяют направленность связей между узлами. Они позволяют найти путь от одного узла к другому, а также установить отношения между узлами – родительское и дочернее.
Различные алгоритмы работы с бинарными деревьями позволяют выполнять различные операции, такие как поиск узла, вставка узла, удаление узла, обход дерева и т.д. Знание узлов и ребер бинарного дерева является основой для понимания и эффективной работы с этой структурой данных.
Корень и листья
Корень в бинарном дереве представляет собой основной элемент, от которого ветвятся все остальные узлы. Он является первым элементом в дереве и не имеет родителя.
Листья, или также называемые терминальными узлами, представляют собой элементы дерева, которые не имеют дочерних узлов. Они находятся в самом нижнем уровне дерева и не разветвляются на другие элементы.
Корень и листья имеют важное значение при работе с бинарными деревьями. Корень позволяет установить начало ветвления и при поиске, добавлении и удалении элементов в дереве, осуществляются операции от корня. Листья же представляют собой конечные элементы дерева и содержат информацию или проводят определенные действия.
Наличие корня и листьев в бинарных деревьях обеспечивает удобство и эффективность работы с данными структурами. Корень служит исходной точкой для обхода дерева и осуществления операций, а листья являются конечными элементами, на которых выполняются необходимые действия.
Глубина и высота
В бинарном дереве глубиной называется максимальное число узлов, которые находятся на пути от корня до какого-либо листа. Глубину можно представить как "дальность" от корня дерева до его наиболее удаленного листа.
Высотой бинарного дерева называется максимальная глубина среди всех его листьев. В отличие от глубины, высоту можно рассматривать как "высоту" дерева, т.е. расстояние от его корня до самого дальнего листа.
Глубина и высота бинарного дерева являются важными характеристиками, которые позволяют оценить его эффективность и сложность алгоритмов, выполняемых над ним.
Рассмотрим глубину и высоту на примере:
Допустим, у нас есть следующее бинарное дерево:
10 / 7 15 / 4 9 20
В этом дереве наибольшая глубина равна 3, так как самый дальний лист находится на третьем уровне.
Высота же этого дерева равна 2, так как наибольшая глубина среди всех листьев равна 2.
Знание глубины и высоты бинарного дерева позволяет оценить скорость работы алгоритмов поиска, добавления и удаления элементов, а также использовать эти параметры во многих алгоритмах и структурах данных.
Особенности бинарного дерева
Бинарное дерево — это структура данных, в которой каждый узел может иметь не более двух потомков. Это одно из самых простых и распространенных типов деревьев, которое широко применяется в информатике.
Одна из основных особенностей бинарного дерева — его гибкость. Благодаря возможности иметь два потомка, каждый узел может быть связан с двумя другими узлами, что позволяет строить различные структуры данных и решать множество задач.
Еще одна особенность бинарного дерева — его эффективность. Благодаря особенностям структуры, операции вставки, поиска и удаления элементов в бинарном дереве могут выполняться за логарифмическое время, что делает его очень быстрым и эффективным инструментом.
Бинарные деревья имеют и свои ограничения. Количество узлов в бинарном дереве ограничено его высотой, что может привести к неправильному балансу дерева и ухудшить его производительность. Однако, при правильном построении и поддержке баланса, бинарное дерево остается эффективной структурой данных.
Бинарное дерево также может быть использовано для построения других типов деревьев и графов. Например, на основе бинарных деревьев можно построить двоичное дерево поиска или хеш-таблицу. Это позволяет улучшить эффективность решения множества задач и оптимизировать работу с данными.
Бинарное дерево — это важная структура данных, которая имеет множество применений и особенностей. Понимание этих особенностей позволяет эффективно использовать бинарные деревья для решения различных задач в информатике и программировании.
Алгоритмы работы с бинарными деревьями
Бинарные деревья — это часто используемая структура данных, которая позволяет эффективно организовывать и хранить информацию. Важным аспектом работы с бинарными деревьями является умение реализовывать различные алгоритмы для работы с этой структурой.
Один из основных алгоритмов работы с бинарными деревьями — это алгоритм обхода дерева. Существует несколько видов обхода дерева: прямой обход (pre-order), симметричный обход (in-order) и обратный обход (post-order). Все эти алгоритмы позволяют посетить каждый узел дерева в определенном порядке.
Алгоритмы обхода дерева обычно реализуются с использованием рекурсии. Для прямого обхода дерева сначала посещается корень, затем левое поддерево, затем правое поддерево. Для симметричного обхода узлы посещаются в порядке левое поддерево, корень, правое поддерево. Для обратного обхода узлы посещаются в порядке левое поддерево, правое поддерево, корень.
Еще одним важным алгоритмом работы с бинарными деревьями является алгоритм поиска элемента. Суть этого алгоритма заключается в поиске элемента в дереве и его возврате. Алгоритм поиска элемента также реализуется с помощью рекурсии. На каждом шаге производится сравнение искомого элемента с текущим узлом, и, в зависимости от результата сравнения, происходит переход к левому или правому поддереву.
Еще одним алгоритмом работы с бинарными деревьями является алгоритм вставки элемента. Он используется для добавления нового элемента в дерево. Алгоритм вставки также реализуется с помощью рекурсии. На каждом шаге происходит сравнение вставляемого элемента с текущим узлом, и, в зависимости от результата сравнения, происходит переход к левому или правому поддереву. Если поддерево пустое, то вставляемый элемент становится новым узлом.
Также существуют и другие алгоритмы работы с бинарными деревьями, например, алгоритм удаления элемента из дерева или алгоритм построения дерева по заданному массиву элементов. Все эти алгоритмы играют важную роль при работе с бинарными деревьями и позволяют эффективно выполнять различные операции с данными.
Примеры применения бинарных деревьев
Бинарные деревья находят широкое применение в различных областях, благодаря своей эффективности и удобной структуре. Вот несколько примеров использования бинарных деревьев:
1. Базы данных:
Бинарные деревья используются для построения индексов в базах данных. Они позволяют быстро находить нужные записи и облегчают выполнение поисковых запросов. Каждый узел дерева содержит ключ и ссылки на два потомка (левый и правый), что обеспечивает эффективное хранение данных.
2. Компиляторы:
Бинарные деревья используются в процессе компиляции программного кода. Они позволяют хранить и организовывать дерево синтаксического разбора, что упрощает анализ и трансформацию кода. Каждый узел дерева представляет отдельное выражение или операцию, а инструкции являются потомками.
3. Сеть:
Бинарные деревья могут быть использованы для построения сетевой топологии. В каждом узле дерева содержатся сведения о сетевых узлах и их связях. Такая структура облегчает маршрутизацию и передачу данных в сети.
4. Интернет-поиск:
Бинарные деревья используются для построения поисковых индексов в системах интернет-поиска. Каждый узел дерева содержит информацию о ключевых словах и ссылках на связанные страницы. Такая структура позволяет эффективно искать информацию в больших массивах данных.
5. Компьютерные игры:
Бинарные деревья могут быть использованы для организации игровых структур, таких как деревья принятия решений или деревья поиска оптимальных ходов. Каждый узел дерева представляет возможное состояние игры, а потомки — возможные следующие ходы. Такая структура позволяет компьютеру эффективно принимать решения и находить оптимальные стратегии.
6. Криптография:
Бинарные деревья могут быть использованы в криптографических алгоритмах для хранения и обработки ключей. Каждый узел дерева содержит ключевую информацию, а потомки — различные операции с ключами, такие как шифрование, расшифровка или проверка подлинности.
Это лишь некоторые примеры применения бинарных деревьев. Их возможности широко используются в различных областях, где требуется эффективное хранение и обработка данных.