n дерево — это структура данных, которая позволяет организовывать информацию и эффективно выполнять операции над ней. Оно основано на идеи иерархического представления данных, где каждый элемент может иметь несколько потомков. Это отличает n дерево от других структур, таких как массивы или односвязные списки, где элементы связаны только двухуточечными ссылками.
n в названии означает, что каждый узел дерева может иметь произвольное количество дочерних элементов. Это позволяет гибко организовывать данные и решать различные задачи, такие как поиск, вставка, удаление элементов. n дерево часто используется в базах данных, операционных системах, компиляторах и других областях информатики.
Для работы с n деревом используются различные алгоритмы и методы. В зависимости от конкретной задачи можно выбрать подходящую реализацию n дерева: бинарное дерево поиска, B-дерево, красно-черное дерево и другие. Каждая из этих реализаций имеет свои особенности и преимущества, что делает их подходящими для разных ситуаций.
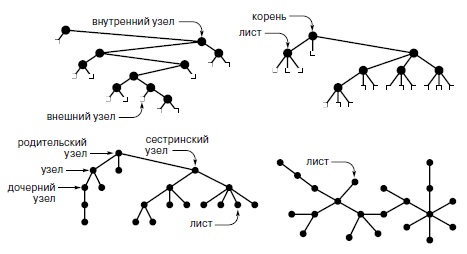
Определение n дерева
Для начала давайте разберемся, что же такое n дерево. n дерево — это структура данных, которая представляет собой иерархическую систему, состоящую из узлов и ребер. Оно является обобщением концепции бинарного дерева, в котором каждый узел может иметь до n дочерних элементов.
Основное отличие n дерева от других структур данных, таких как связанный список или массив, заключается в его иерархической природе. Узлы n дерева имеют прямой доступ только к своим потомкам, и каждый узел может иметь любое количество потомков, ограниченное только значением n. Это позволяет эффективно представлять иерархическую информацию и выполнять различные операции, такие как поиск, вставка и удаление элементов.
Структура n дерева состоит из узлов и ребер. Каждый узел имеет значение и ссылки на своих потомков. Корень n дерева — это основной узел, от которого начинается иерархия. Каждый узел имеет свое значение и ссылки на своих потомков, если они существуют. Узлы без потомков называются листьями.
Характеристики n дерева:
| Структура | Иерархическая |
| Количество потомков у узла | Ограничено значением n |
| Доступ к потомкам | Прямой доступ |
| Корень | Основной узел |
| Узлы без потомков | Листья |
n дерево находит широкое применение в программировании. Оно используется для организации и хранения иерархических данных, таких как файловые системы, деревья поиска, базы данных и прочее. Операции поиска, вставки и удаления элементов в n дереве эффективны и позволяют обрабатывать большие объемы данных.
Однако использование n дерева также имеет свои преимущества и недостатки. Среди преимуществ можно отметить высокую эффективность операций, возможность хранения иерархических данных и легкость масштабирования. Однако недостатками являются сложность реализации и управления n деревом, а также сложность работы с большими иерархиями данных.
B-дерево
Структура и характеристики n дерева
Прежде чем погрузиться в подробности, давайте рассмотрим общую структуру и характеристики n дерева. N дерево является иерархической структурой данных, в которой каждый узел может иметь произвольное количество потомков. Оно состоит из корня и набора узлов, которые связаны между собой с помощью ребер.
Узел n дерева состоит из двух основных компонентов: ключа и списка потомков. Ключ — это значение, которое хранится в узле, и используется для его идентификации и сравнения с другими узлами. Список потомков содержит ссылки на узлы, которые являются прямыми потомками данного узла.
Каждый узел n дерева может иметь от 0 до n потомков, что делает его гибкой структурой данных. Это позволяет эффективно организовывать и хранить большие объемы данных, а также обеспечивает легкость вставки и удаления элементов.
Узлы n дерева могут быть разделены на уровни, начиная с корневого узла на уровне 0. Путь от корневого узла до любого другого узла называется простым путем, и его длина равна количеству ребер на этом пути. Глубина дерева — это максимальная длина простого пути от корня до любого из его листьев. Дерево с одним узлом имеет глубину 0.
Ключевая характеристика n дерева — сбалансированность. Это означает, что разница в глубине между любыми двумя листьями не должна быть слишком велика. Сбалансированное n дерево обеспечивает эффективный поиск, вставку и удаление элементов, что делает его особенно полезным в программировании.
Пример структуры n дерева:
Корень: узел A
Потомки корня: узел B, узел C, узел D, узел E
Потомки узла B: узел F, узел G
Потомки узла C: узел H, узел I
Потомки узла D: узел J
Потомки узла E: узел K, узел L, узел M
Таким образом, n дерево представляет собой иерархическую структуру данных с гибким количеством потомков узлов. Это позволяет эффективно организовывать и хранить данные, а также обеспечивает быстрый и удобный доступ к элементам дерева.
Применение n дерева в программировании
Дерево является одной из наиболее важных структур данных в программировании. Оно широко применяется в реализации различных алгоритмов и задач, связанных с организацией и хранением информации.
Хранение и поиск данных
Одним из основных применений n дерева является хранение и поиск данных. За счет своей структуры, дерево позволяет эффективно организовать и хранить большое количество элементов. Ключевая особенность n дерева заключается в том, что оно обеспечивает быстрый доступ к элементам за счет быстрого поиска. Например, при поиске определенного элемента в дереве, время выполнения операции будет пропорционально глубине дерева, что является очень эффективным.
Сортировка данных
Другим важным применением n дерева является его использование для сортировки данных. Дерево позволяет упорядочить элементы по ключу или значению, что делает его необходимым инструментом для решения множества задач связанных с сортировкой. Например, при добавлении нового элемента в дерево, оно автоматически сортирует его в нужной позиции, что упрощает обработку данных.
Балансировка дерева
Еще одно важное применение n дерева в программировании — балансировка дерева. Балансировка дерева позволяет поддерживать оптимальное распределение элементов, что обеспечивает оптимальное время выполнения операций. Например, при добавлении или удалении элементов в дерево, происходит перераспределение элементов, чтобы сохранить баланс.
| Преимущества применения n дерева в программировании | Недостатки применения n дерева в программировании |
|---|---|
|
|
Применение n дерева в программировании является очень полезным и широко используется для решения множества задач. Оно обеспечивает эффективность операций и позволяет удобно работать со структурами данных, что делает его незаменимым инструментом в разработке программного обеспечения.
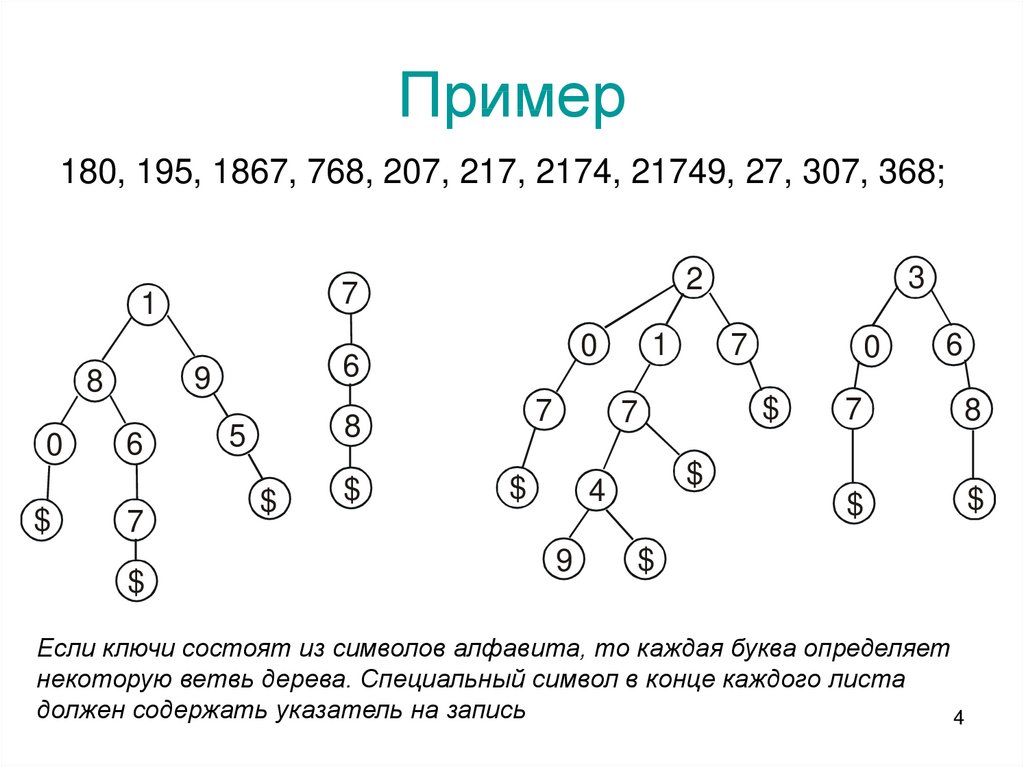
Поиск и вставка элементов в n дерево
Поиск и вставка элементов в n дерево – это одна из основных операций, которые можно выполнять с данным типом структуры данных. N дерево — это древовидная структура данных, в которой каждый узел может иметь произвольное количество потомков, от 0 до n, где n — максимальное количество потомков у узла.
В процессе поиска элемента в n дереве, начиная с корневого узла, происходит сравнение искомого значения со значениями узлов. Если искомое значение меньше значения текущего узла, то поиск продолжается в левом поддереве, если больше – в правом поддереве. Если значение совпадает, значит, элемент найден.
При вставке элемента в n дерево происходит поиск места для вставки с использованием тех же самых правил, что и при поиске. Если место для вставки найдено, новый элемент создается в виде нового узла и добавляется к имеющемуся дереву.
Одно из преимуществ использования n дерева заключается в том, что операции поиска и вставки выполняются средним образом за логарифмическое время O(log n), что делает его эффективным для работы с большими объемами данных.
| Преимущества | Недостатки |
|---|---|
|
|
Удаление элементов из n дерева
Удаление элементов из n дерева — одна из основных операций, которая может выполняться над этой структурой данных. Для удаления элемента из n дерева можно выполнить следующие шаги:
- Найти элемент, который нужно удалить. Для этого обычно используется алгоритм поиска.
- Если элемент не найден, то операция удаления не может быть выполнена.
- Если элемент найден, то проверить, является ли он листом (узел без дочерних элементов) или внутренним узлом (узел с одним или двумя дочерними элементами).
- Если элемент является листом, то его можно просто удалить из дерева.
- Если элемент является внутренним узлом, то нужно определить его наибольшего потомка в поддереве, либо наименьшего потомка, в зависимости от спецификации n дерева.
- Заменить удаляемый элемент на наибольший (или наименьший) потомок.
- Удалить наибольший (или наименьший) потомок из его исходного местоположения.
В процессе удаления элементов из n дерева необходимо учитывать и обновлять связи между узлами. После удаления элемента, структура дерева должна оставаться корректной, то есть должны быть сохранены все свойства n дерева.
Удаление элементов из n дерева является важной операцией при работе с этой структурой данных, так как позволяет управлять его содержимым и обеспечивать эффективное использование памяти.
Однако, при удалении элементов из n дерева необходимо учитывать возможные проблемы, связанные с нарушением баланса дерева и ухудшением его производительности. Поэтому, при разработке алгоритмов удаления элементов из n дерева необходимо уделить внимание оптимизации и соблюдению всех правил и условий этой операции.
Преимущества и недостатки использования n дерева
Преимущества:
1. Эффективность поиска
n дерево обеспечивает эффективность операции поиска элементов. Благодаря особенностям структуры дерева, поиск происходит за время O(log n), где n — количество элементов в дереве. Это делает n дерево особенно полезным для задач, требующих быстрого поиска и сортировки данных.
2. Вставка и удаление элементов
Вставка и удаление элементов в n дереве протекают также эффективно, как и поиск. Время выполнения операций вставки и удаления составляет O(log n), что позволяет легко обновлять и модифицировать структуру дерева при изменении данных.
3. Балансировка
n дерево имеет особенность самобалансировки. Это означает, что структура дерева автоматически поддерживает оптимальное распределение элементов, что в свою очередь обеспечивает равномерность операций поиска, вставки и удаления. Благодаря этому, n дерево гарантирует высокую производительность даже при большой нагрузке.
4. Поддержка многопоточности
Некоторые реализации n дерева обеспечивают поддержку многопоточности. Это позволяет использовать дерево параллельно нескольким потокам, что повышает эффективность работы с общими данными и сокращает время выполнения операций.
Недостатки:
1. Сложность реализации
Реализация n дерева может быть несколько сложной задачей, особенно при его более сложных вариациях, таких как B-дерево или красно-черное дерево. Корректная реализация требует определенных навыков и понимания работы алгоритмов. Ошибка в реализации может привести к неправильному функционированию дерева и ошибкам в результатах операций.
2. Потребление памяти
n дерево может потреблять большой объем памяти. Каждый узел дерева требует дополнительной памяти для хранения данных и указателей на следующие узлы. При большом количестве элементов дерево может занимать значительное место в памяти, что может быть проблематично в случае ограниченных ресурсов или работы с большими объемами данных.
3. Сложность обновления
Обновление данных в n дереве может быть сложным процессом. При изменении элементов дерева или вставке новых элементов может потребоваться перебалансировка структуры дерева. Операции перебалансировки могут быть затратными по времени и ресурсам, особенно для больших деревьев.
Не смотря на некоторые недостатки, n дерево остается одной из наиболее эффективных структур данных для работы с большими объемами данных и требовательными задачами поиска и сортировки.