Деревья — это структуры данных, которые широко используются в программировании. Они играют важную роль во многих алгоритмах и приложениях, позволяя эффективно организовывать и хранить данные. В программировании существует несколько видов деревьев, каждый из которых имеет свои особенности и применения.
Одним из наиболее распространенных видов деревьев является двоичное дерево. Как следует из названия, двоичное дерево состоит из узлов, каждый из которых имеет максимум два потомка. Это свойство делает его особенно полезным для реализации поисковых алгоритмов, таких как двоичный поиск. Каждый узел в двоичном дереве имеет ссылку на левого и правого потомка, а также значение, которое он содержит.
Еще одним интересным видом деревьев является красно-черное дерево. Красно-черное дерево является сбалансированным двоичным деревом, в котором узлы могут быть красными или черными. Это дает дополнительные ограничения на структуру дерева, что позволяет эффективно выполнять операции вставки, удаления и поиска. Красно-черные деревья используются во многих алгоритмах и структурах данных, таких как ассоциативные массивы и множества.
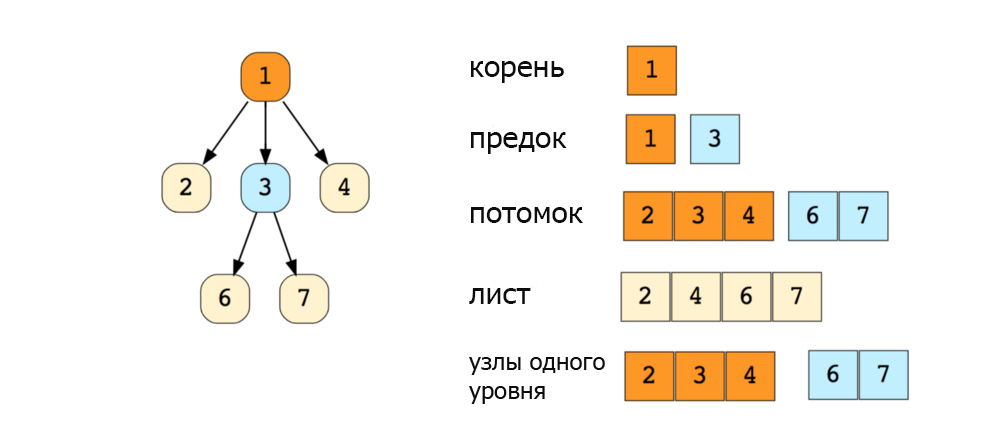
Дерево поиска в ширину
Дерево поиска в ширину (BFS) — это один из алгоритмов обхода или поиска данных в дереве. Он используется для поиска или обхода элементов в порядке их удаленности от корня дерева. BFS обеспечивает постепенный поиск элементов, начиная от корня и постепенно расширяясь на ближайшие элементы, прежде чем переходить к следующему уровню.
В BFS элементы дерева обходятся по уровням, то есть сначала обрабатываются все узлы первого уровня, затем второго, третьего и так далее. Это позволяет наглядно представить дерево и упрощает поиск и обработку данных.
Алгоритм работы
Алгоритм BFS основан на использовании очереди (queue) для хранения пройденных элементов и множества (set) для отслеживания посещенных узлов. Процесс обхода в ширину состоит из следующих шагов:
- Начать с корневого узла и добавить его в очередь;
- Пока очередь не станет пустой, повторять следующие шаги:
- Извлечь первый элемент из очереди и проверить, является ли он искомым элементом;
- Если элемент найден, то поиск завершается;
- Если элемент не найден, добавить все непосещенные дочерние элементы текущего узла в очередь;
Таким образом, BFS идет от корня дерева и проверяет все его дочерние узлы перед переходом к следующему уровню. Это гарантирует, что все элементы находятся наименее удаленными от корня на текущем уровне, перед переходом к более удаленным элементам.
Дерево поиска в ширину широко применяется для нахождения кратчайшего пути между элементами дерева, обхода или поиска данных и других задач, где необходимо постепенно расширять область поиска.
Тренировки по алгоритмам от Яндекса. Лекция 8: «Деревья»
Двоичное дерево поиска
Двоичное дерево поиска (Binary Search Tree, BST) – одна из самых распространенных структур данных, используемых в программировании. Оно представляет собой иерархическую структуру, состоящую из узлов, где каждый узел имеет значение и два потомка — левый и правый.
Главная особенность двоичного дерева поиска заключается в том, что оно поддерживает эффективную операцию поиска, вставки и удаления элементов. Каждый узел дерева содержит значение, которое больше значения его левого потомка и меньше значения его правого потомка. Это правило позволяет выполнять эффективный поиск элементов, делая промежуточные проверки и сокращая количество операций.
Для вставки элемента в двоичное дерево поиска необходимо сравнить его значение с корневым узлом. Если оно меньше, то оно помещается в левое поддерево, если больше — в правое. Вставка происходит рекурсивно, пока не будет найдено подходящее место.
Удаление элемента из двоичного дерева поиска также осуществляется через сравнение значений. Если узел имеет двух потомков, то он заменяется минимальным элементом из правого поддерева или максимальным из левого. Если у узла только один потомок или он является листом, то он удаляется непосредственно.
| Пример двоичного дерева поиска: |
|---|
 |
Двоичное дерево поиска может использоваться для решения различных задач, включая упорядоченное хранение и быстрый поиск данных. Оно применяется в алгоритмах сортировки, поиска, кэширования и в различных системах баз данных.
Однако недостатком двоичного дерева поиска является возможность его деградации в несбалансированное дерево, что может привести к снижению производительности операций. Для устранения этой проблемы существуют различные виды сбалансированных двоичных деревьев, такие как AVL-дерево и красно-черное дерево.
AVL-дерево
AVL-дерево — это один из видов сбалансированных двоичных деревьев поиска. Оно было разработано Георгом Адельсон-Вельским и Евгением Ландисом в 1962 году. Название AVL образовано из первых букв инициалов создателей.
AVL-дерево отличается от обычного двоичного дерева поиска тем, что оно всегда является сбалансированным. Сбалансированность достигается путем поддержания равновесия высот поддеревьев. В AVL-дереве разница в высотах левого и правого поддерева любого узла не превышает 1.
Для поддержания сбалансированности AVL-дерева при вставке или удалении элементов из дерева, автоматически выполняются операции поворота и балансировки дерева. Повороты осуществляют изменение структуры дерева путем перемещения узлов, что позволяет поддерживать оптимальную сбалансированность. Балансировка выполняется с помощью поворотов и обновления высот поддеревьев.
Преимущества использования AVL-дерева включают быстрый поиск, вставку и удаление элементов. Время выполнения основных операций в AVL-дереве составляет O(log n), где n — количество элементов в дереве.
AVL-дерево находит широкое применение в различных областях, где требуется эффективное хранение и обработка данных. Оно используется в базах данных, поисковых движках, компиляторах, сортировках и других алгоритмах. Благодаря своей сбалансированной структуре, AVL-дерево является надежным инструментом для организации и управления данными в программировании.
| Преимущества AVL-дерева | Недостатки AVL-дерева |
|---|---|
| Быстрый поиск, вставка и удаление элементов | Требуется дополнительная память для хранения высот поддеревьев |
| Гарантированная сбалансированность | Сложность реализации и поддержки |
| Эффективное управление данными | Ограниченная поддержка большого объема данных |

Красно-черное дерево
Красно-черное дерево является одной из самых популярных структур данных в программировании. Оно является сбалансированным деревом поиска, где каждый узел имеет одну из двух окрасок: красную или черную.
Основная идея красно-черного дерева заключается в поддержании некоторых инвариантов, которые гарантируют балансировку дерева. В частности, все пути от корня до листьев должны содержать одинаковое количество черных узлов, а красные узлы не могут идти подряд.
Эти инварианты позволяют достичь эффективного выполнения операций вставки, удаления и поиска элементов в дереве. Благодаря балансировке, время выполнения этих операций в красно-черном дереве остается логарифмическим и гарантированно не растет с ростом количества элементов.
Преимущества красно-черного дерева:
1. Эффективность операций: благодаря балансировке красно-черное дерево обеспечивает быстрое выполнение операций вставки, удаления и поиска элементов.
2. Гарантированный логарифмический рост: время выполнения операций не зависит от количества элементов в дереве, что делает его предпочтительным выбором для хранения больших объемов данных.
3. Универсальность: красно-черное дерево может быть использовано для различных задач, включая хранение упорядоченных данных, реализацию словарей и множеств, а также в алгоритмах комбинаторики и графов.
Недостатки красно-черного дерева:
1. Дополнительное использование памяти: каждый узел красно-черного дерева содержит не только свои данные, но и информацию о цвете. Это приводит к некоторому дополнительному использованию памяти.
2. Сложность реализации: реализация красно-черного дерева требует более сложного кода по сравнению с другими структурами данных. Требуется аккуратность при изменении структуры дерева и поддержании его балансировки.
Красно-черное дерево является мощным инструментом в программировании и широко применяется в различных областях. Оно обеспечивает эффективное выполнение операций и гарантированно поддерживает балансировку, что делает его предпочтительным выбором при работе с большими объемами данных.
Суффиксное дерево
Суффиксное дерево – это структура данных в программировании, используемая для эффективного хранения и обработки строковых данных. Оно представляет собой особый тип дерева, которое представляет все возможные суффиксы данной строки.
Суффиксное дерево имеет множество применений, включая строковый поиск, алгоритмы сжатия данных, анализ последовательностей ДНК и т.д. Оно позволяет выполнять поиск подстроки в строке за линейное время, а также решать множество других задач с использованием эффективных алгоритмов.
Структура суффиксного дерева основана на понятии префиксного дерева (трие). Каждый узел дерева представляет суффикс исходной строки, а каждое ребро содержит символ, который добавляется к предыдущей строке для формирования следующего суффикса.
Преимущества суффиксного дерева включают его компактность, эффективность поиска и поддержку множества операций над строками. Оно позволяет решать сложные задачи, связанные с обработкой строковых данных, и часто используется в биоинформатике, анализе текстов и других областях, где требуется быстрый и эффективный поиск подстрок.
Суффиксное дерево является важным концептом в программировании, и его понимание может помочь разработчику решить сложные задачи, связанные с обработкой строк и анализом данных. Изучение суффиксных деревьев позволяет расширить навыки программирования и научиться эффективно применять их в различных областях.

B-дерево
B-дерево (B-tree) — это сбалансированное дерево поиска, которое широко применяется в базах данных и файловых системах для эффективного хранения и поиска данных. Оно было разработано в 1970 году Рудольфом Баэром и стало одной из основных структур данных, используемых в компьютерных системах.
Основное преимущество B-дерева заключается в его способности эффективно обрабатывать большие объемы данных и поддерживать эффективное выполнение операций вставки, удаления и поиска. B-дерево обладает хорошей производительностью при работе с диском, так как обеспечивает минимизацию операций записи и чтения на жесткий диск.
Основные свойства B-дерева:
- Каждый узел B-дерева может содержать несколько ключей и указателей на дочерние узлы.
- Уровни дерева сбалансированы, то есть все внутренние узлы должны иметь одинаковое количество потомков.
- Ветвление дерева позволяет эффективно разделить пространство ключей между узлами.
- Каждый узел имеет ограничение на максимальное количество ключей.
- Ключи в узле упорядочены по возрастанию, что упрощает бинарный поиск.
- Узлы между уровнями связаны указателями, что позволяет операциям поиска и изменения быстро перемещаться по дереву.
В B-дереве ключи представляют собой значения, по которым происходит поиск данных, а значения — сами данные. Оно поддерживает операции вставки новых ключей, удаления существующих ключей и поиска данных по ключу.
B-дерево является ключевой структурой данных для организации хранилища данных во многих базах данных и файловых системах. Оно обеспечивает высокую производительность и эффективное использование памяти, что делает его незаменимым инструментом при работе с большими объемами данных.