Бинарное дерево – это иерархическая структура данных, состоящая из узлов, соединенных ребрами. Каждый узел может иметь не более двух потомков: левого и правого. Такое ограничение позволяет нам эффективно организовывать и обрабатывать данные в бинарном дереве.
Степень бинарного дерева определяется как максимальное количество потомков, которые может иметь узел. Для бинарного дерева степень всегда равна двум, так как каждый узел может иметь только двух потомков — левого и правого.
Степень бинарного дерева – это важный показатель его структуры. Он влияет на операции по вставке, удалению и поиску элементов в дереве. Чем больше степень дерева, тем больше места требуется для его хранения. Однако, большая степень может улучшить производительность операций, особенно при работе с большими объемами данных.
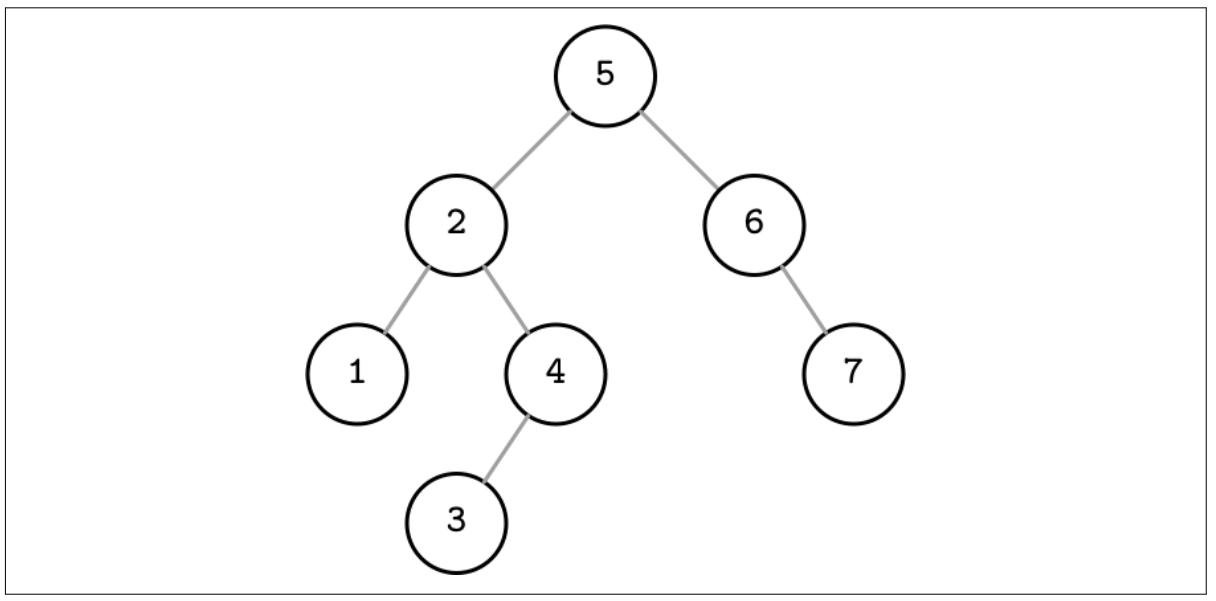
Что такое бинарное дерево
Бинарное дерево — это структура данных, состоящая из узлов, связанных между собой направленными ребрами. В бинарном дереве каждый узел может иметь максимум два потомка — левого и правого. Левый потомок находится слева от родительского узла, а правый — справа. Узлы, не имеющие потомков, называются листьями.
Бинарные деревья широко используются в информатике и программировании для эффективного хранения и организации данных. Они позволяют выполнять быстрый поиск, вставку и удаление элементов, а также предоставляют удобные и эффективные алгоритмы для обхода и работы с данными.
Преимуществом бинарного дерева является его удобная структура, позволяющая разделить элементы на две группы с помощью двух потомков. Это упрощает поиск нужного элемента и улучшает производительность операций с данными.
Бинарное дерево может быть использовано для различных задач, например, для организации иерархической структуры данных, поиска и сортировки информации, реализации алгоритмов компиляторов и многое другое.
Для визуализации и работы с бинарным деревом нужно использовать таблицу. Каждый узел представляет собой строку таблицы, содержащую информацию о значении узла и ссылки на его потомков.
В целом, бинарное дерево является важным инструментом в программировании и представляет собой эффективную структуру данных для работы с большими объемами информации. Понимание его принципов и особенностей позволяет эффективно решать различные задачи в области программирования.
#20. Реализация бинарного дерева на Python | Структуры данных
Что определяет степень бинарного дерева
Степень бинарного дерева определяется максимальным числом дочерних узлов, которые могут быть прямыми потомками для каждого узла дерева. То есть она показывает, сколько дочерних узлов может иметь каждый узел в дереве.
Степень бинарного дерева может быть различной и может быть задана заранее или изменена в процессе построения дерева. Она влияет на структуру и характеристики дерева, а также на возможности его использования.
Однократная степень
Если степень бинарного дерева равна 1, то это означает, что каждый узел может иметь только одного прямого потомка. Такое дерево называется крайним и состоит из одной или нескольких ветвей, где каждый узел имеет только одного потомка. Однократные бинарные деревья часто используются для реализации списков или последовательностей, где каждый элемент имеет ссылку только на следующий элемент.
Двукратная степень
Когда степень бинарного дерева равна 2, каждый узел может иметь двух прямых потомков. Такое бинарное дерево называется полным или сбалансированным, потому что все узлы имеют одинаковую степень и дерево выглядит симметрично. Полные бинарные деревья широко применяются в алгоритмах сортировки и поиска, так как они обеспечивают быстрый доступ к данным.
Таким образом, степень бинарного дерева является важным параметром, определяющим его характеристики и возможности использования. Различные степени бинарных деревьев подходят для различных задач и могут быть выбраны в зависимости от конкретных требований при проектировании и использовании структур данных.
Виды степеней бинарного дерева
Бинарное дерево – это структура данных, в которой каждый узел может иметь не более двух потомков. Степень бинарного дерева определяет максимальное количество потомков, которые может иметь каждый узел в этом дереве.
Существуют различные виды степеней бинарного дерева:
| Степень | Описание |
|---|---|
| Степень 0 | Узел не имеет потомков (лист дерева). |
| Степень 1 | Узел имеет только одного потомка. |
| Степень 2 | Узел имеет двух потомков. Это наиболее распространенная степень бинарного дерева. |
| Степень n | Узел имеет n потомков. |
Степень бинарного дерева играет важную роль при анализе и работы с такими структурами данных. От степени дерева зависит его вместимость и эффективность работы алгоритмов, которые используют это дерево.
Применение бинарных деревьев с разными степенями зависит от конкретных задач и требований. В некоторых случаях более высокая степень может увеличить производительность, но при этом потребуется больше памяти для хранения структуры.
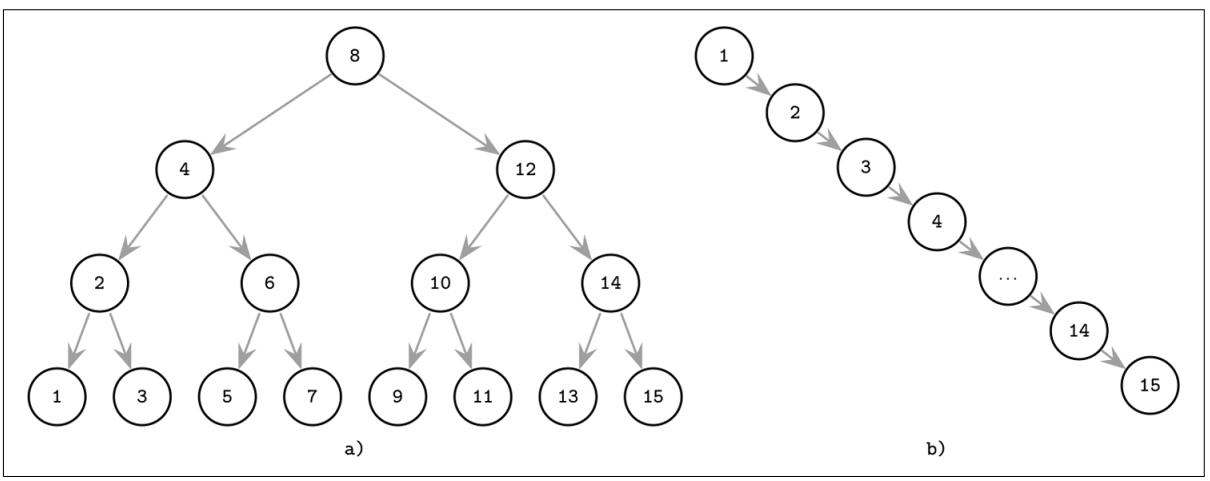
Зависимость размера дерева от его степени
Степень бинарного дерева является одной из основных характеристик, определяющих его структуру и свойства. Понимание зависимости размера дерева от его степени является важным аспектом при проектировании и анализе таких деревьев.
В бинарном дереве каждый узел может иметь максимум двух потомков – левого и правого. Степень дерева определяется максимальным количеством потомков, которые может иметь каждый узел. Например, степень 2 означает, что узел может иметь до двух потомков, степень 3 – до трех и так далее.
Зависимость размера дерева от его степени очевидна – чем больше степень дерева, тем больше узлов оно может содержать. Поэтому, чем выше степень дерева, тем более «плотное» оно становится. Максимальное количество узлов в бинарном дереве с заданной степенью можно вычислить по формуле: M = 2^h — 1, где M – максимальное количество узлов, h – степень дерева.
Пример
Рассмотрим пример с бинарным деревом степени 2. У нас есть корень, у которого есть два потомка – левый и правый. У каждого из этих потомков также могут быть свои потомки, но не более двух. Таким образом, на каждом уровне дерева количество узлов увеличивается в два раза. Если мы знаем степень дерева и глубину (количество уровней), мы можем вычислить максимальное количество узлов, которое дерево может содержать.
Знание зависимости размера дерева от его степени позволяет оптимизировать структуру и процессы работы с бинарными деревьями. Например, для хранения больших объемов данных может быть целесообразно выбрать дерево с более высокой степенью.
Таким образом, понимание зависимости размера дерева от его степени является важным аспектом при разработке и использовании бинарных деревьев. Оно помогает оптимизировать структуру дерева и выбрать наиболее подходящую степень в зависимости от поставленных задач.
Какова роль степени бинарного дерева
Степень бинарного дерева играет важную роль в его структуре и функциональности. Она определяет количество дочерних узлов, которые может иметь каждый узел в дереве.
Степень бинарного дерева может быть равна 0, 1 или 2. Если степень равна 0, то узлы не имеют дочерних элементов и представляют собой листья дерева. Если степень равна 1, то каждый узел имеет только одного дочернего элемента. Если степень равна 2, то каждый узел имеет два дочерних элемента.
Различные степени бинарного дерева предоставляют разные возможности для работы с данными. Например, в дереве с нулевой степенью мы можем хранить только листья и работать с ними, не обращаясь к внутренним узлам. В дереве со степенью 1 у нас есть возможность хранить дочерние элементы только на одном уровне, что может быть полезно, когда нам необходим доступ только к определенному поддереву. В дереве со степенью 2 мы можем строить полноценные бинарные деревья, где каждый узел имеет два дочерних элемента и мы можем легко выполнять операции вставки, удаления и поиска данных.
Роль степени бинарного дерева заключается в определении ограничений на количество дочерних узлов, что позволяет нам контролировать структуру дерева и его поведение. Оптимальный выбор степени зависит от конкретных требований и характеристик данных, с которыми мы работаем. Некоторые алгоритмы и приложения могут быть эффективнее при использовании деревьев с определенной степенью, поэтому правильный выбор степени бинарного дерева является важным аспектом проектирования и оптимизации структур данных.
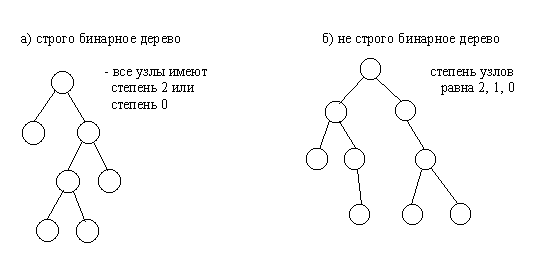
Применение бинарных деревьев с разными степенями
Бинарные деревья с разными степенями имеют широкий спектр применений в различных областях. Они используются как основа для реализации различных алгоритмов и структур данных.
Одним из основных применений бинарных деревьев с разными степенями является их использование в системах управления базами данных. Эти деревья позволяют эффективно организовать хранение и поиск данных, обеспечивая быстроту выполнения запросов и изменений в базе данных.
Также бинарные деревья с разными степенями находят применение в алгоритмах сортировки и поиска. Например, алгоритмы сортировки слиянием, быстрой сортировки и сортировки вставками используют бинарные деревья для эффективной организации и обработки данных.
Еще одним важным применением бинарных деревьев с разными степенями является их использование в компьютерной графике и графических интерфейсах. Они используются для представления и обработки графических объектов, таких как деревья сцен, графики и изображения.
Бинарные деревья с разными степенями могут также использоваться в искусственном интеллекте для решения сложных задач. Они могут быть применены в областях машинного обучения, обработки естественного языка и распознавания образов.
В целом, бинарные деревья с разными степенями являются мощным инструментом, который может быть использован во множестве областей. Их гибкость и эффективность делают их незаменимым элементом при разработке и оптимизации различных алгоритмов и структур данных. Знание и понимание применения бинарных деревьев с разными степенями позволяет создавать эффективные и масштабируемые программные решения.