Дерево — это одна из наиболее простых и понятных структур данных. Граф, который является деревом, обладает несколькими важными свойствами.
Во-первых, в дереве нет циклов, то есть невозможно обойти все его вершины так, чтобы возвращение в исходную вершину было возможно. Во-вторых, дерево должно быть связным, то есть из любой вершины должны быть достижимы все остальные вершины графа. Также, дерево может быть ориентированным или неориентированным, т.е. из одной вершины могут исходить несколько ребер или только одно.
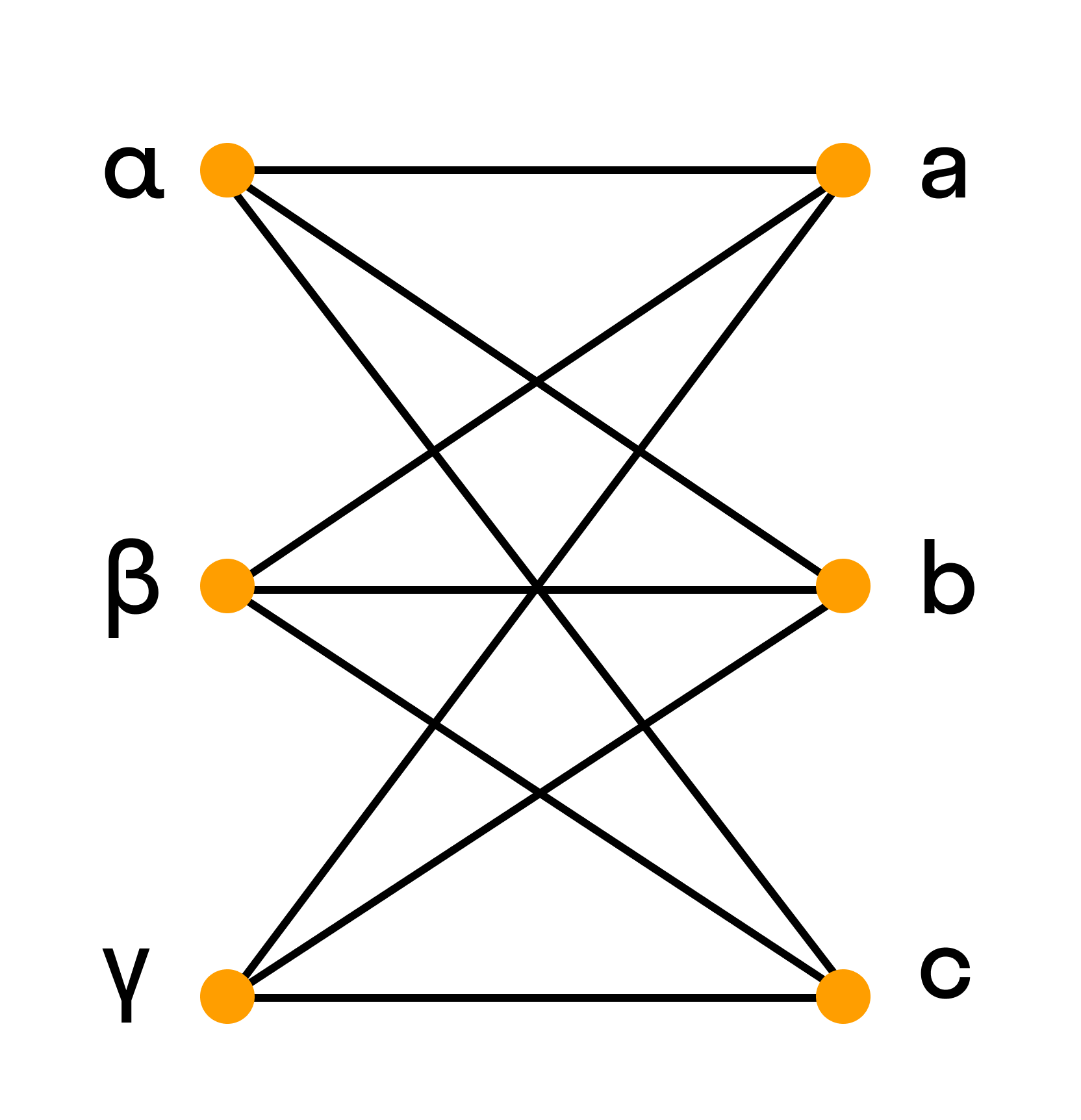
Жирные точки в графах обозначают вершины, а отрезки — ребра. Вершины соединяются между собой ребрами, образуя структуру графа. Граф, в котором все вершины соединены ребрами, называется полным. Однако, не все полные графы являются деревьями. Дерево — это уникальное подмножество полного графа, удовлетворяющее вышеописанным свойствам. Таким образом, для определения, является ли граф деревом, необходимо проверить его структуру и связность.
Выбирая все графы, которые являются деревьями, необходимо обратить внимание на условия, которые они должны удовлетворять. Деревом может быть одиночная вершина без ребер, граф из нескольких вершин, соединенных ребрами, а также любое подмножество полного графа, удовлетворяющее определению дерева. Умение выбирать и распознавать деревья в графах является одним из ключевых навыков в программировании и алгоритмах обработки данных.
Что такое графы и деревья?
Графы и деревья являются абстрактными структурами данных, которые широко используются в информатике и математике для представления и анализа связей между объектами. Они являются частными случаями графовых структур.
Графы
Граф – это математическая структура, состоящая из множества вершин и множества ребер, которые устанавливают связи между вершинами. Вершины представляют отдельные объекты, а ребра определяют отношения и связи между ними.
Графы могут быть ориентированными, где ребра имеют направление, или неориентированными, где ребра не имеют направления. В графах могут существовать различные типы ребер, такие как однонаправленные, двунаправленные или взвешенные.
Графы могут использоваться для моделирования различных сетей и связей в различных областях, таких как транспортные сети, социальные сети, компьютерные сети и т.д. Они позволяют анализировать и оптимизировать связи и пути между вершинами.
Деревья
Дерево – это частный случай графа, где каждая пара вершин соединена единственным ребром, и на графе нет циклов. Вершина графа, не имеющая входящих ребер, называется корнем дерева.
Деревья также могут быть ориентированными или неориентированными. В деревьях используется понятие поддерева – группы вершин и ребер, которые сами по себе являются деревом.
Деревья широко применяются для организации данных и анализа иерархических структур. Они используются в операционных системах для представления файловой системы, в базах данных для представления данных и в алгоритмах поиска и сортировки.
Понимание графов и деревьев является важным фундаментом для решения различных задач в информатике и математике. Их изучение позволяет развивать абстрактное мышление и решать сложные проблемы.
ВСЯ теория по графам для олимпиад
Как выбрать графы, которые являются деревьями?
Для того чтобы выбрать графы, которые являются деревьями, необходимо понимать, что такое графы и деревья.
Граф — это математическая абстракция, представляющая собой совокупность вершин и ребер, связывающих эти вершины. В графах можно выделить подграфы, которые называются деревьями.
Дерево — это связный граф без циклов. Вершины дерева называются узлами, а ребра — ветвями. В деревьях есть одна вершина, которая не имеет входящих ребер, и она называется корнем дерева. Каждый узел дерева имеет ровно одного предка, за исключением корня, у которого предков нет.
Чтобы выбрать графы, которые являются деревьями, нужно проверить, удовлетворяют ли они определению дерева. Важными характеристиками деревьев являются наличие ровно одной связной компоненты и отсутствие циклов.
Если граф удовлетворяет этим условиям, то он можно считать деревом. Чтобы найти все деревья в графе, можно использовать различные алгоритмы, такие как обход в глубину или обход в ширину.
Таким образом, выбрать графы, которые являются деревьями, несложно, если знать основные понятия и характеристики деревьев. Наличие одной связной компоненты и отсутствие циклов помогут определить, является ли граф деревом или нет.
Что означают жирные точки в графах?
Жирные точки в графах обозначают вершины, которые являются отрезками ребер. Они отличаются от обычных точек, которые представляют собой просто соединения между вершинами. Жирные точки имеют больший вес и важность в графе, так как они служат опорными точками для построения пути или алгоритма.
Вершина — это один из базовых элементов графа, который представляет отдельный объект или узел. Вершины могут быть связаны друг с другом с помощью ребер, которые представляют собой линии или отрезки. Часто вершины графа обозначают как точки на плоскости, для удобства визуализации и работы с ними.
Отрезок ребра — это связь между двумя вершинами графа. Он может быть направленным или ненаправленным, в зависимости от того, есть ли стрелка или нет. Ребра могут иметь разные веса или стоимости, которые отражают их значимость или сложность.
Жирные точки, как уже было сказано, являются особенными вершинами в графе. Они могут указывать на ключевые моменты или важные узлы в системе, которые требуют особого внимания. Жирные точки могут также использоваться для выделения точек входа или выхода из системы, где необходимо особо акцентировать внимание.
Использование жирных точек в графах позволяет удобно визуализировать и анализировать сложные системы, выделять ключевые компоненты и выявлять связи между ними. Они помогают лучше понять структуру и функциональность графа, а также использовать его в различных алгоритмах и задачах.
В итоге, жирные точки в графах играют важную роль, обозначая вершины, которые являются отрезками ребер. Они помогают выделить и выявить ключевые компоненты графа, упрощают его анализ и улучшают понимание его структуры и функциональности.
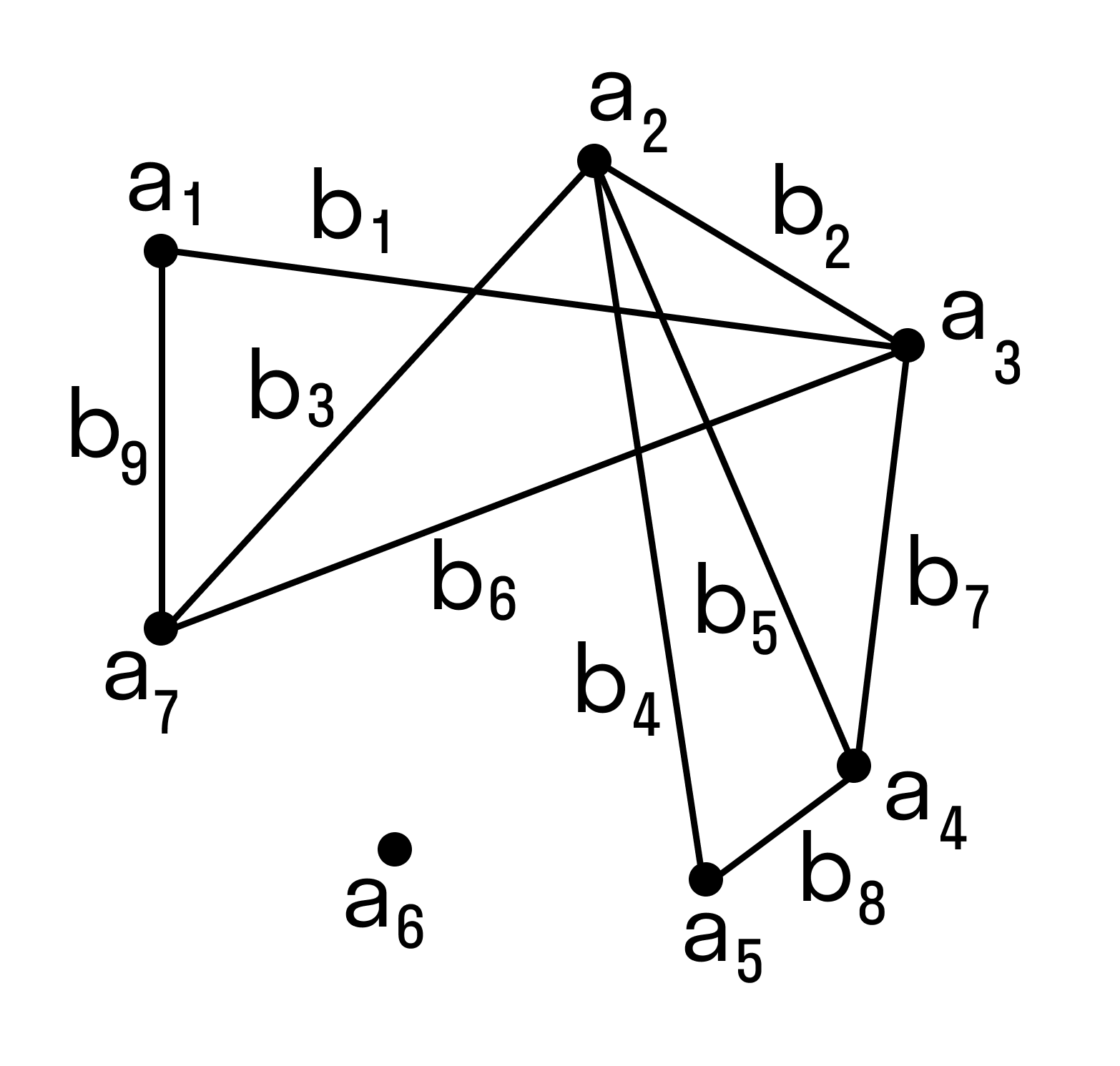
Вершины, отрезки и ребра в графах
Граф — это абстрактная математическая структура, состоящая из множества вершин (или узлов) и набора ребер, которые связывают эти вершины. Вершины обозначаются точками, а ребра — отрезками, соединяющими эти точки.
Каждая вершина графа может иметь связи с другими вершинами или же не иметь их. Эти связи, или ребра, представляют собой отношения, которые могут быть направленными или ненаправленными. Если ребра имеют направление, то граф называется ориентированным, в противном случае он является неориентированным.
Ребра в графе представляют собой пути или связи между двумя вершинами. Они могут быть представлены различными способами — например, стрелками, линиями или ломаными линиями. Ребра также могут быть помечены весами или метками, которые указывают на характеристики или свойства соответствующих связей. Например, ребра могут иметь вес, который определяет длину или стоимость соединения между вершинами.
Примеры вершин, отрезков и ребер в графах:
Возьмем в качестве примера граф, представляющий дерево. В этом графе вершины обозначаются точками, а отрезки (или ребра) — линиями, соединяющими эти точки. Например, мы можем представить дерево с пятью вершинами в виде следующего графа:
| Вершины (точки) | Отрезки (ребра) |
|---|---|
| 1 | 1-2 |
| 2 | 1-3 |
| 3 | 2-4 |
| 4 | 2-5 |
| 5 |
В этом примере у нас есть пять вершин, обозначенных числами от 1 до 5. Ребра, или отрезки, обозначаются соединяющими их числами. Например, ребро между вершинами 1 и 2 обозначается как "1-2".
Таким образом, вершины, отрезки и ребра являются основными элементами графа и позволяют представить его структуру и связи между его компонентами.
Подводя итоги:
Вершины, отрезки и ребра играют важную роль в представлении графов. Вершины представляют собой точки, отрезки — связи между этими точками, а ребра — пути или связи между вершинами. Они позволяют наглядно представить структуру графа и понять его взаимосвязи.
Примеры графов, являющихся деревьями
Деревья в графах – это особый тип связного ориентированного графа, в котором отсутствуют циклы. Такие графы имеют множество применений в различных областях, начиная от информатики и программирования, и заканчивая логистикой и коммуникационными сетями.
Рассмотрим несколько примеров графов, являющихся деревьями:
Пример 1:
Граф 1:
Вершины: A, B, C, D
Ребра: AB, BC, CD
Данный граф состоит из четырех вершин и трех ребер. Он удовлетворяет определению дерева, так как не содержит циклов. Здесь нет возможности пройти по ребрам в графе, начиная с одной вершины, и вернуться в эту вершину, не проходя при этом ни по какому ребру дважды.
Граф 1:
Вершины: X, Y, Z, W
Ребра: XY, XZ, XW
Этот граф также является деревом, так как удовлетворяет условию отсутствия циклов. В данном графе можно начать с вершины X, двигаться по ребрам и вернуться обратно в X, пройдя при этом по каждому ребру только один раз.
Пример 3:
Граф 3:
Вершины: 1, 2, 3, 4, 5
Ребра: 1-2, 1-3, 2-4, 2-5
Данный граф также является деревом, так как обладает отсутствием циклов. Можно начать с вершины 1 и перемещаться по ребрам графа, так чтобы каждое ребро было пройдено только один раз.
Таким образом, приведенные примеры демонстрируют, что графы могут быть деревьями, если они удовлетворяют условию отсутствия циклов. Важность анализа деревьев в графах объясняется их широким спектром применений и полезностью в решении разнообразных задач.